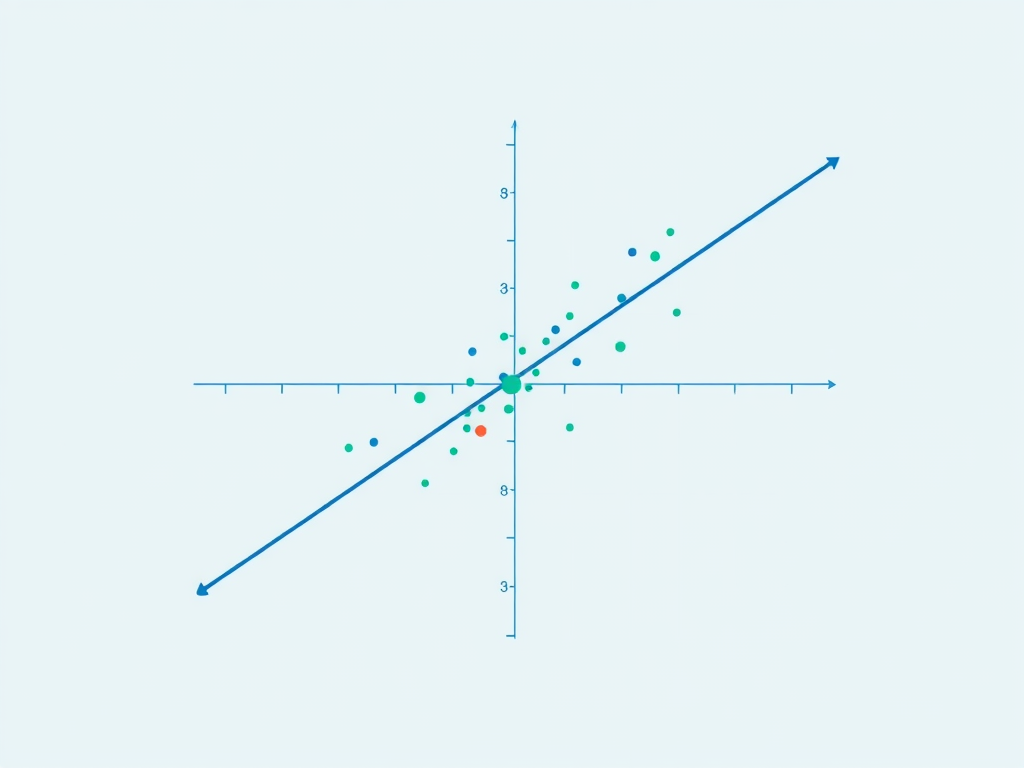
La regresión lineal es una de las técnicas más utilizadas en ciencia de datos para modelar y predecir relaciones entre variables. Su simplicidad, interpretabilidad y eficacia la convierten en una herramienta esencial para los científicos de datos que buscan comprender patrones en los datos y hacer predicciones informadas.

¿Qué es la Regresión Lineal?

La regresión lineal se basa en la premisa de que existe una relación lineal entre una variable dependiente (o de respuesta) y una o más variables independientes (o predictoras). La forma más común de regresión lineal es la regresión lineal simple, que involucra una sola variable independiente, mientras que la regresión lineal múltiple utiliza múltiples variables independientes.

Ecuación de la Regresión Lineal

La ecuación de la regresión lineal simple se expresa como: $$\begin{equation} y = \beta_0 + \beta_1 x + \epsilon \end{equation}$$

donde:

• \(y\) es la variable dependiente.
• \(x\) es la variable independiente.
• \(\beta_0\) es la intersección (término constante).
• \(\beta_1\) es la pendiente (coeficiente) que indica el cambio en y por cada unidad de cambio en x.
• \(\epsilon\) es el término de error que captura la variabilidad no explicada.

Proceso de Implementación en Ciencia de Datos

1. Recolección de Datos

Los datos pueden provenir de diversas fuentes, como bases de datos, APIs, archivos CSV o incluso web scraping. Es crucial asegurarse de que los datos sean relevantes y estén limpios antes de proceder.

2. Exploración de Datos

Antes de aplicar la regresión lineal, es esencial realizar un análisis exploratorio de datos (EDA). Esto incluye:

• Visualización de datos mediante gráficos de dispersión para identificar relaciones.
• Cálculo de estadísticas descriptivas.
• Detección de outliers y valores atípicos.

3. Preprocesamiento de Datos

El preprocesamiento puede incluir:

• Normalización o estandarización de variables.
• Manejo de valores faltantes.
• Transformaciones de variables si se requiere linealidad.

4. Construcción del Modelo

Utilizando bibliotecas como scikit-learn en Python, se puede construir el modelo de regresión lineal. Aquí se estima los coeficientes (ββ) que minimizan el error cuadrático medio.

5. Evaluación del Modelo

La evaluación del modelo se realiza utilizando métricas como:

• R² (coeficiente de determinación): Indica la proporción de la varianza en la variable dependiente que es predecible a partir de las variables independientes.
• RMSE (raíz del error cuadrático medio): Proporciona una medida de la magnitud del error en las predicciones.

6. Interpretación de Resultados

Los coeficientes del modelo ofrecen información sobre la relación entre las variables. Un coeficiente positivo indica que a medida que la variable independiente aumenta, la variable dependiente también lo hace, mientras que un coeficiente negativo sugiere lo contrario.

7. Predicciones

Una vez validado el modelo, se puede utilizar para realizar predicciones sobre nuevos datos, lo que permite tomar decisiones informadas basadas en los resultados obtenidos.

Aplicaciones en Ciencia de Datos

La regresión lineal tiene múltiples aplicaciones en ciencia de datos, tales como:

• Análisis de Ventas: Predecir ventas futuras basándose en factores como el marketing y la estacionalidad.
• Economía: Modelar el impacto de variables económicas en el crecimiento del PIB.
• Salud: Relacionar factores de riesgo con resultados de salud, como la presión arterial y el colesterol.
• Marketing: Evaluar el impacto de la inversión publicitaria en el retorno de la inversión (ROI).

---

Aplicación de Regresión Lineal en Python

La regresión lineal es una técnica poderosa y accesible en el arsenal de un científico de datos. Su capacidad para modelar relaciones lineales y hacer predicciones precisas la convierte en una herramienta fundamental para el análisis de datos. A medida que los proyectos de ciencia de datos se vuelven más complejos, la regresión lineal a menudo sirve como un punto de partida para explorar relaciones más avanzadas y métodos predictivos.