La matriz de covarianza es una herramienta fundamental en estadística y análisis de datos que permite entender la relación entre múltiples variables. Es especialmente relevante en el contexto de la estadística multivariante, donde se estudian conjuntos de datos con múltiples dimensiones. Este artículo explora qué es la matriz de covarianza, cómo se calcula, y sus diversas aplicaciones en diferentes campos.

¿Qué es la Matriz de Covarianza?

La matriz de covarianza es una generalización de la varianza para múltiples variables. Mientras que la varianza mide la dispersión de una sola variable, la covarianza mide cómo dos variables cambian juntas.

Definición Matemática

Para un conjunto de nn observaciones de pp variables, la matriz de covarianza \(\Sigma\) se define como: $$\Sigma = \frac{1}{n-1} (X - \bar{X})^T (X - \bar{X})$$

donde:

1. \(X\) es la matriz de datos, con cada fila representando una observación y cada columna representando una variable.
2. \(\bar{X}\) es el vector de medias de las variables.

La entrada \(\sigma_{ij}\) de la matriz de covarianza se calcula como: $$\sigma_{ij} = \text{Cov}(X_i, X_j) = \frac{1}{n-1} \sum_{k=1}^{n} (x_{ik} - \bar{x_i})(x_{jk} - \bar{x_j})$$

donde \(x_{ik}\) y \(x_{jk}\) son las observaciones de las variables \(i\) y \(j\) respectivamente.

Propiedades de la Matriz de Covarianza

• Simetría: La matriz de covarianza es simétrica, es decir, \(\sigma_{ij}=\sigma_{ji}\)
• Dimensiones: Si hay \(p\) variables, la matriz de covarianza es de tamaño \(p \times p\).
• Valores Propios: Los valores propios de la matriz de covarianza son siempre no negativos, lo que significa que la matriz es semidefinida positiva.

Aplicaciones de la Matriz de Covarianza

La matriz de covarianza tiene múltiples aplicaciones en diferentes campos:

1. Análisis de Datos Multivariantes

En análisis de datos, la matriz de covarianza es fundamental para entender la relación entre múltiples variables. Ayuda a identificar qué variables están correlacionadas y en qué medida.

2. Análisis de Componentes Principales (PCA)

El PCA es una técnica de reducción de dimensionalidad que utiliza la matriz de covarianza para identificar las direcciones (componentes principales) en las que los datos tienen la mayor varianza. Esto es útil para simplificar los datos mientras se conserva la mayor cantidad de información posible.

3. Modelos de Regresión

En modelos de regresión, la matriz de covarianza de los coeficientes estimados se utiliza para calcular errores estándar y pruebas de hipótesis, lo que permite evaluar la significancia estadística de los predictores.

4. Optimización de Portafolios en Finanzas

En el ámbito financiero, la matriz de covarianza se utiliza para la optimización de portafolios. Permite evaluar el riesgo y la rentabilidad esperada de diferentes combinaciones de activos, ayudando a los inversores a tomar decisiones informadas.

5. Control de Calidad

En control de calidad, la matriz de covarianza se utiliza para analizar la variabilidad de múltiples características de un producto, ayudando a identificar áreas donde se pueden realizar mejoras.

6. Machine Learning

En el aprendizaje automático, la matriz de covarianza se utiliza en algoritmos como el Análisis Discriminante Lineal (LDA) y en la regularización de modelos para evitar el sobreajuste.

Caso de Uso: Análisis de las Características de las Flores Iris

Aquí tienes un ejemplo de código en Python que ilustra el uso de la matriz de covarianza en un caso práctico. En este caso, utilizaremos un conjunto de datos de características de flores (el famoso conjunto de datos Iris) para entender cómo se relacionan las diferentes características entre sí.

El objetivo es calcular la matriz de covarianza entre las características de las flores Iris y utilizarla para entender la relación entre estas características. Esto puede ser útil, por ejemplo, para la clasificación de especies de flores.

1. Importar las bibliotecas necesarias

1. pandas: Gestión de datos
2. seaborn: Visualización de datos estadísticos
3. matplotlib para realizar los gráficos.

2. Carga de Datos

Usamos seaborn para cargar el conjunto de datos Iris, que incluye características de flores como la longitud y el ancho del sépalo y del pétalo.

3. Visualización de Datos

Mostramos las primeras filas del conjunto de datos para tener una idea de su estructura.

4. Calcular la matriz de covarianza

Calculamos la matriz de covarianza para las cuatro características de las flores.

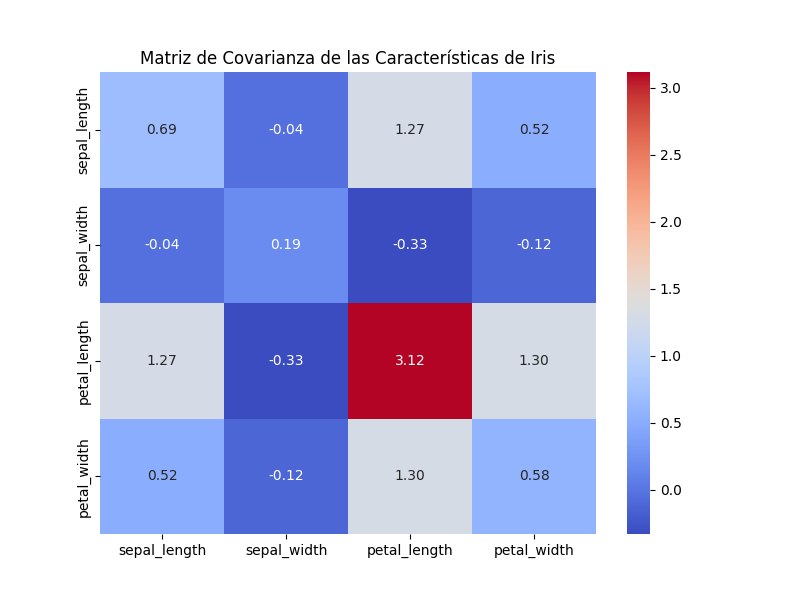
5. Visualización de la Matriz de Covarianza:

Utilizamos un heatmap para visualizar la matriz de covarianza, lo que facilita la identificación de relaciones entre las variables.

# 1. Importar las bibliotecas necesarias
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 2. Cargar el conjunto de datos Iris
iris = sns.load_dataset('iris')

# 3. Mostrar las primeras filas del conjunto de datos
print("Primeras filas del conjunto de datos Iris:")
print(iris.head())

# 4. Calcular la matriz de covarianza
cov_matrix = iris[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']].cov()

# Mostrar la matriz de covarianza
print("\nMatriz de Covarianza:")
print(cov_matrix)

# 5. Visualizar la matriz de covarianza utilizando un heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(cov_matrix, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('Matriz de Covarianza de las Características de Iris')
plt.show()

Mira el código completo aquí

---

La matriz de covarianza es una herramienta fundamental en estadística y análisis de datos, proporcionando información valiosa sobre la relación entre múltiples variables. Sus aplicaciones abarcan desde análisis de datos multivariantes hasta finanzas y machine learning. Comprender la matriz de covarianza y su uso puede proporcionar una base sólida para realizar análisis más complejos y tomar decisiones informadas en diversos campos.