Se utiliza para realizar transformaciones sobre vectores o puntos en un espacio

La matriz de transformación es un concepto utilizado en matemáticas y en diversas disciplinas como la geometría, la computación gráfica y la ciencia de datos. Se refiere a una matriz que se utiliza para realizar transformaciones sobre vectores o puntos en un espacio, como rotaciones, escalados, traslaciones y reflexiones.

Tipos de Transformaciones

1. Transformaciones Afines:

1. Traslación: Mueve un punto o un objeto a lo largo de un vector.
2. Escalado: Cambia el tamaño de un objeto, aumentando o disminuyendo sus dimensiones.
3. Rotación: Gira un objeto alrededor de un punto específico.
4. Reflexión: nvierte un objeto a través de un eje.

2. Transformaciones Lineales:

1. Cambian la forma o la posición de un objeto en el espacio sin alterar la estructura del mismo.

Representación

La matriz de transformación se representa generalmente como una matriz cuadrada. Por ejemplo, en un espacio bidimensional (2D), una matriz de transformación puede tener la siguiente forma. $$ T = \begin{pmatrix} a & b\\ c & d \end{pmatrix}$$

Donde \(\textit{a, b, c y d}\) son coeficientes que determinan el tipo de transformación que se aplicará a un vector \(\begin{pmatrix} x\\ y \end{pmatrix}\)

Ejemplos:

1. Rotación en 2D:

La matriz de rotación para un ángulo \(\theta\) es: $$R = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix}$$

1. Rotación en 2D:

La matriz de escalado sería: $$S = \begin{pmatrix} s_x & 0 \\ 0 & s_y \end{pmatrix}$$ Donde \(s_x\) y \(s_y\) son los factores de escalado en las direcciones x e y.

Ejemplos en Python:

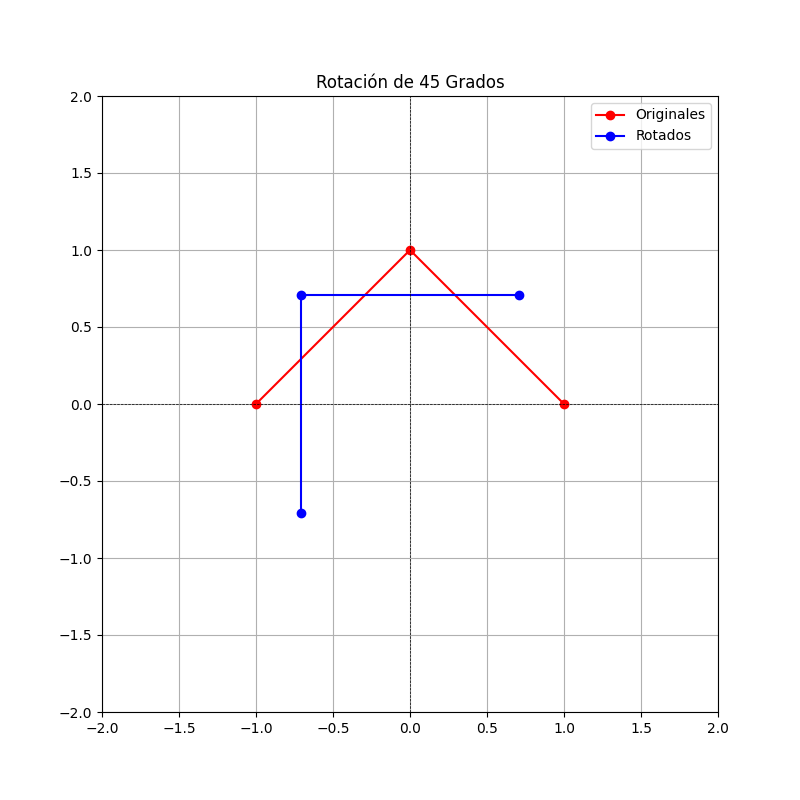
Vamos a definir un conjunto de puntos, aplicar una matriz de rotación y visualizar el resultado utilizando matplotlib.

# Importación de las bibliotecas necesarias:
# numpy para operaciones numéricas y manejo de matrices.
# matplotlib.pyplot para la creación de gráficos.
import numpy as np
import matplotlib.pyplot as plt

# Definir los puntos originales (un triángulo en este caso)
puntos = np.array([[1, 0], [0, 1], [-1, 0]])

# Definir el ángulo de rotación en grados
angulo = 45
theta = np.radians(angulo)  # Convertir a radianes

# Matriz de rotación
R = np.array([[np.cos(theta), -np.sin(theta)],
              [np.sin(theta), np.cos(theta)]])

# Aplicar la transformación
puntos_rotados = puntos @ R.T  # Transponer R para multiplicar correctamente

# Graficar los puntos originales y rotados
plt.figure(figsize=(8, 8))
plt.plot(puntos[:, 0], puntos[:, 1], 'ro-', label='Originales')
plt.plot(puntos_rotados[:, 0], puntos_rotados[:, 1], 'bo-', label='Rotados')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.axhline(0, color='black',linewidth=0.5, ls='--')
plt.axvline(0, color='black',linewidth=0.5, ls='--')
plt.grid()
plt.gca().set_aspect('equal', adjustable='box')
plt.title(f'Rotación de {angulo} Grados')
plt.legend()
plt.show()

Mira el código completo aquí

---

La matriz de transformación es una herramienta fundamental en matemáticas y sus aplicaciones prácticas. Permite manipular y entender cómo los puntos y objetos se pueden mover y cambiar en el espacio, lo que es esencial en campos como la geometría, la física y la ingeniería de software.

Las matrices de transformación son herramientas fundamentales en ciencia de datos, facilitando la manipulación, análisis y visualización de datos. Su aplicación en diversas áreas, desde la preparación de datos hasta el modelado y la interpretación, las convierte en un componente esencial en el flujo de trabajo de un científico de datos.