Este artículo analiza el sistema de fracciones del Ojo de Horus desde una perspectiva aritmética moderna. Exploramos cómo los antiguos egipcios codificaron una serie geométrica de razón \(1/2\) en un símbolo mitológico, anticipando intuitivamente el concepto de límite y convergencia, y cómo esta estructura servía tanto para propósitos administrativos como metafísicos.

1. El Enigma de la Unidad Perdida

¿Es posible que la suma de todas las partes de un todo nunca llegue a completar el todo? Esta paradoja, que atormentó a Zenón de Elea siglos después, parece haber sido comprendida y aceptada por los escribas del Reino Antiguo. En el corazón de la administración egipcia se encontraba el Heqat, una unidad de medida de volumen para granos, cuya subdivisión no era aleatoria, sino que seguía una progresión elegante y sagrada: las fracciones del Ojo de Horus.

2. Anatomía de una Progresión Geométrica

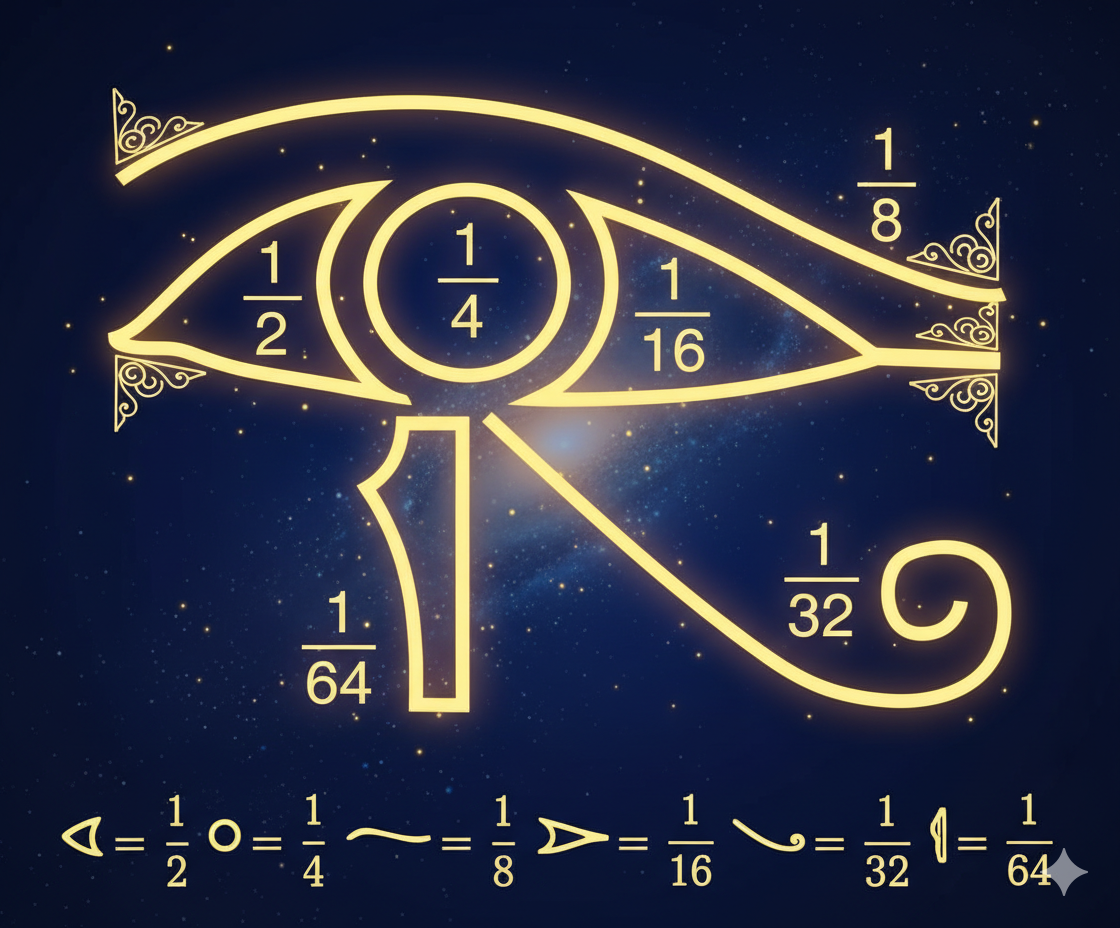
Según el mito, el ojo de Horus fue despedazado por Set y luego restaurado por Thot. Sin embargo, la restauración no fue perfecta. Matemáticamente, el ojo se divide en seis partes, cada una representando una fracción de potencia de dos:

• La pupila: \(1/4\)
• La ceja: \(1/8\)
• El lado izquierdo: \(1/2\)
• El lado derecho: \(1/16\)
• La cola curva: \(1/32\)
• La lágrima: \(1/64\)

Formalmente, podemos definir estas partes como los términos de una progresión geométrica \(a_n = (\frac{1}{2})^n\) para \(n \in \{1, 2, 3, 4, 5, 6\}\). La suma de estas partes es:

$$\sum_{n=1}^{6} \frac{1}{2^n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} = \frac{63}{64}$$

3. La Intuición del Límite

Lo más fascinante para el matemático profesional no es la suma en sí, sino el \(1/64\) faltante. La mitología atribuye el resto faltante a la "magia de Thot". Desde el análisis matemático, esto es una ilustración finita de una serie convergente. Si extendiéramos este proceso al infinito, obtendríamos:

$$\lim_{k \to \infty} \sum_{n=1}^{k} \frac{1}{2^n} = 1$$

Los egipcios utilizaban esta "imperfección" deliberada. El \(1/64\) restante no era un error de cálculo, sino un recordatorio de que la perfección absoluta pertenece al plano de lo divino, mientras que la aritmética aplicada se detiene en la precisión necesaria para el comercio y la ofrenda.

4. Conexiones y Legado

Este sistema de potencias de dos negativas es el antepasado conceptual de nuestro sistema binario moderno. La eficiencia de dividir por mitades sucesivas permitió a una civilización sin notación decimal manejar inventarios complejos con una precisión asombrosa.

¿Podríamos considerar el Ojo de Horus como el primer gráfico de visualización de datos de la historia? Representa la partición del espacio y la materia de una forma que es, simultáneamente, arte, religión y ciencia pura.

Figuras Conceptuales Sugeridas

Figura 1: Desglose Anatómico-Matemático. Una ilustración del Ojo de Horus donde cada trazo (la ceja, la pupila, la lágrima) está etiquetado con su fracción correspondiente y su valor decimal, mostrando la jerarquía visual de las potencias de dos.

Figura 2: La Recta Numérica de Horus. Una representación en una recta real entre 0 y 1, donde se visualiza cómo cada fracción sucesiva va "saltando" la mitad de la distancia restante hacia la unidad, destacando gráficamente el espacio vacío del \(1/64\) final.

Figura 3: Mapa de Calor de Convergencia. Un diagrama de áreas donde un cuadrado unidad se va subdividiendo recursivamente según las fracciones del ojo, permitiendo ver cómo la suma de las áreas casi llena el cuadrado original.

Referencias

• Chace, A. B. (1927). The Rhind Mathematical Papyrus. Mathematical Association of America.
• Ritter, J. (2002). Egyptian Mathematics. En: Selin, H. (eds) Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures.
• Imhausen, A. (2016). Mathematics in Ancient Egypt: A Contextual History. Princeton University Press.