Subplots y Múltiples Figuras con Matplotlib: Layouts Complejos
Aprende a crear layouts complejos con múltiples gráficos usando subplots, GridSpec y técnicas avanzadas de organización visual.
¡Organiza tus visualizaciones como un profesional! En este tutorial aprenderás a crear layouts complejos con múltiples gráficos, utilizando subplots, GridSpec y técnicas avanzadas para organizar la información de manera efectiva.
Objetivo: Dominar la creación de figuras con múltiples subgráficos, controlando layouts, espaciado y organización visual para presentaciones impactantes.
Índice
- Introducción a Subplots
- Subplots Básicos
- Función subplots()
- GridSpec para Layouts Complejos
- Ejes Compartidos
- Subplots Anidados
- Control de Espaciado
- Layouts Personalizados
- Casos de Uso Avanzados
Introducción a Subplots
Los subplots permiten mostrar múltiples gráficos en una sola figura, facilitando la comparación y el análisis de datos relacionados.
¿Por qué usar Subplots?
- Comparación: Visualizar diferentes aspectos de los mismos datos
- Análisis Multivariable: Mostrar relaciones entre múltiples variables
- Espacio Eficiente: Maximizar el uso del espacio disponible
- Narrativa Visual: Contar una historia completa con datos
- Publicaciones: Formato ideal para papers científicos
Conceptos Básicos
- Figure: Contenedor principal que puede tener múltiples subplots
- Axes: Área individual donde se dibuja cada gráfico
- Subplot: Combinación de figure y axes para un gráfico específico
- Grid: Sistema de coordenadas para posicionar subplots
Subplots Básicos
Comienza con la función subplot() para crear arreglos simples de gráficos.
Subplot Básico
import matplotlib.pyplot as plt
import numpy as np
# Datos
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)
y4 = np.cos(x + np.pi/4)
plt.figure(figsize=(12, 8))
# Crear 4 subplots en una cuadrícula 2x2
plt.subplot(2, 2, 1) # Fila 1, Columna 1
plt.plot(x, y1, 'b-', linewidth=2)
plt.title('sin(x)')
plt.grid(True, alpha=0.3)
plt.subplot(2, 2, 2) # Fila 1, Columna 2
plt.plot(x, y2, 'r-', linewidth=2)
plt.title('cos(x)')
plt.grid(True, alpha=0.3)
plt.subplot(2, 2, 3) # Fila 2, Columna 1
plt.plot(x, y3, 'g-', linewidth=2)
plt.title('sin(x + π/4)')
plt.grid(True, alpha=0.3)
plt.subplot(2, 2, 4) # Fila 2, Columna 2
plt.plot(x, y4, 'm-', linewidth=2)
plt.title('cos(x + π/4)')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Diferentes Arreglos
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y = np.sin(x)
plt.figure(figsize=(15, 10))
# Arreglo 1x3
plt.subplot(1, 3, 1)
plt.plot(x, y, 'b-', linewidth=2)
plt.title('1x3 - Gráfico 1')
plt.grid(True, alpha=0.3)
plt.subplot(1, 3, 2)
plt.plot(x, y**2, 'r-', linewidth=2)
plt.title('1x3 - Gráfico 2')
plt.grid(True, alpha=0.3)
plt.subplot(1, 3, 3)
plt.plot(x, np.sqrt(np.abs(y)), 'g-', linewidth=2)
plt.title('1x3 - Gráfico 3')
plt.grid(True, alpha=0.3)
# Arreglo 3x1
plt.figure(figsize=(8, 12))
plt.subplot(3, 1, 1)
plt.plot(x, y, 'b-', linewidth=2)
plt.title('3x1 - Gráfico 1')
plt.grid(True, alpha=0.3)
plt.subplot(3, 1, 2)
plt.plot(x, y**2, 'r-', linewidth=2)
plt.title('3x1 - Gráfico 2')
plt.grid(True, alpha=0.3)
plt.subplot(3, 1, 3)
plt.plot(x, np.sqrt(np.abs(y)), 'g-', linewidth=2)
plt.title('3x1 - Gráfico 3')
plt.grid(True, alpha=0.3)
plt.tight_layout()
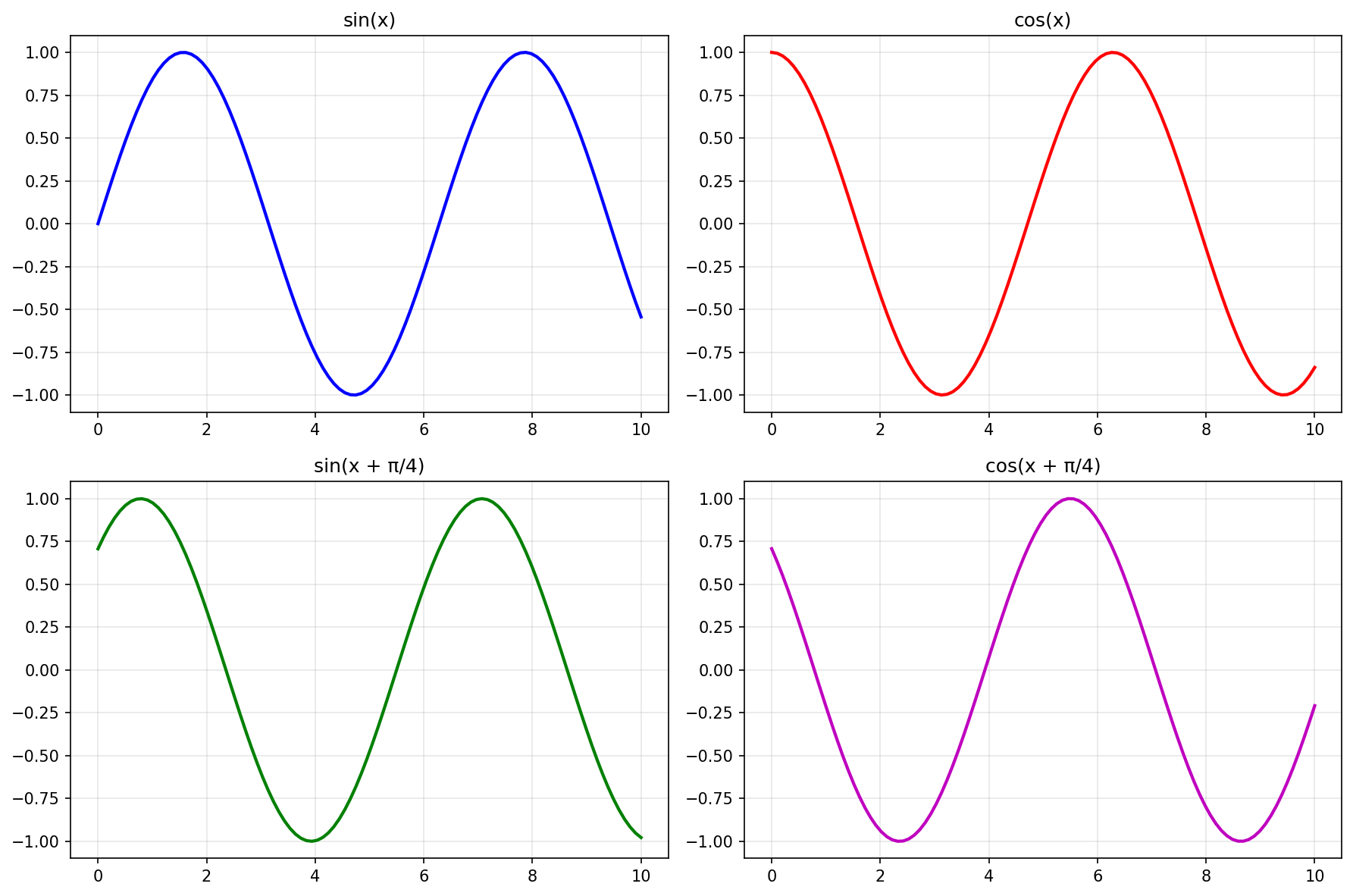
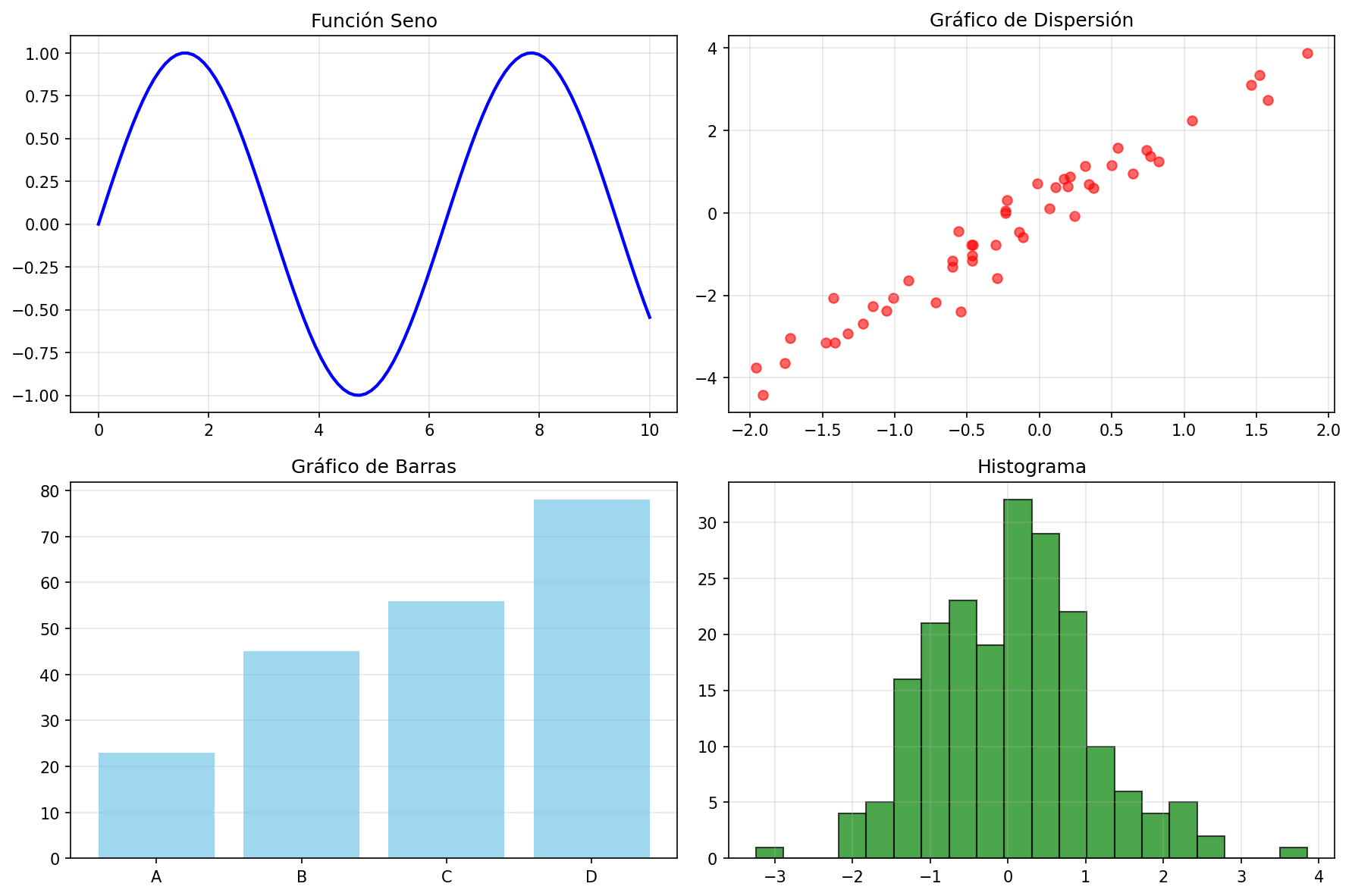
plt.show() Fig. 1: Ejemplo de subplots básicos organizados en cuadrícula 2x2
Fig. 1: Ejemplo de subplots básicos organizados en cuadrícula 2x2
Función subplots()
La función subplots() es más conveniente para crear múltiples subplots y ofrece mayor control.
Subplots con Tuplas
import matplotlib.pyplot as plt
import numpy as np
# Crear figura y ejes en una sola llamada
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(12, 8))
# Datos
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)
y4 = np.cos(x + np.pi/4)
# Graficar en cada subplot
ax1.plot(x, y1, 'b-', linewidth=2)
ax1.set_title('sin(x)')
ax1.grid(True, alpha=0.3)
ax2.plot(x, y2, 'r-', linewidth=2)
ax2.set_title('cos(x)')
ax2.grid(True, alpha=0.3)
ax3.plot(x, y3, 'g-', linewidth=2)
ax3.set_title('sin(x + π/4)')
ax3.grid(True, alpha=0.3)
ax4.plot(x, y4, 'm-', linewidth=2)
ax4.set_title('cos(x + π/4)')
ax4.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Acceso por Índice
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
# Datos
x = np.linspace(0, 10, 100)
# Acceder a cada subplot por índice
for i in range(2):
for j in range(3):
y = np.sin(x + (i*3 + j) * np.pi/6)
axes[i, j].plot(x, y, linewidth=2)
axes[i, j].set_title(f'φ = {(i*3 + j) * 30}°')
axes[i, j].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Aplanar Arrays de Ejes
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(3, 2, figsize=(12, 10))
# Aplanar el array de ejes para iterar fácilmente
axes_flat = axes.flatten()
x = np.linspace(0, 10, 100)
for i, ax in enumerate(axes_flat):
y = np.sin(x + i * np.pi/3)
ax.plot(x, y, linewidth=2, color=f'C{i}')
ax.set_title(f'Subplot {i+1}')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()GridSpec para Layouts Complejos
GridSpec permite crear layouts más flexibles y complejos que los subplots tradicionales.
GridSpec Básico
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
# Crear GridSpec
fig = plt.figure(figsize=(12, 8))
gs = gridspec.GridSpec(3, 3, figure=fig)
# Datos
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)
# Crear subplots con diferentes tamaños
ax1 = fig.add_subplot(gs[0, :]) # Ocupa toda la primera fila
ax1.plot(x, y1, 'b-', linewidth=2)
ax1.set_title('Gráfico Principal (fila completa)')
ax1.grid(True, alpha=0.3)
ax2 = fig.add_subplot(gs[1, 0]) # Esquina inferior izquierda
ax2.plot(x, y2, 'r-', linewidth=2)
ax2.set_title('Gráfico Secundario 1')
ax2.grid(True, alpha=0.3)
ax3 = fig.add_subplot(gs[1, 1]) # Centro inferior
ax3.plot(x, y3, 'g-', linewidth=2)
ax3.set_title('Gráfico Secundario 2')
ax3.grid(True, alpha=0.3)
ax4 = fig.add_subplot(gs[1:, 2]) # Ocupa las dos últimas filas de la última columna
ax4.plot(x, y1 * y2, 'm-', linewidth=2)
ax4.set_title('Producto de Funciones')
ax4.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()GridSpec con Espaciado Personalizado
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
fig = plt.figure(figsize=(14, 10))
# GridSpec con espaciado personalizado
gs = gridspec.GridSpec(4, 4, figure=fig,
wspace=0.3, hspace=0.4, # Espaciado horizontal y vertical
left=0.1, right=0.9, # Márgenes izquierdo y derecho
top=0.9, bottom=0.1) # Márgenes superior e inferior
x = np.linspace(0, 10, 100)
# Subplot grande en el centro
ax_main = fig.add_subplot(gs[1:3, 1:3])
ax_main.plot(x, np.sin(x), 'b-', linewidth=3)
ax_main.set_title('Gráfico Principal', fontsize=14, fontweight='bold')
ax_main.grid(True, alpha=0.3)
# Subplots más pequeños alrededor
ax1 = fig.add_subplot(gs[0, 0])
ax1.plot(x, np.cos(x), 'r-', linewidth=2)
ax1.set_title('Superior Izquierda')
ax1.grid(True, alpha=0.3)
ax2 = fig.add_subplot(gs[0, 1:3])
ax2.plot(x, np.sin(x + np.pi/4), 'g-', linewidth=2)
ax2.set_title('Superior Centro')
ax2.grid(True, alpha=0.3)
ax3 = fig.add_subplot(gs[0, 3])
ax3.plot(x, np.cos(x + np.pi/4), 'm-', linewidth=2)
ax3.set_title('Superior Derecha')
ax3.grid(True, alpha=0.3)
ax4 = fig.add_subplot(gs[1:3, 0])
ax4.plot(x, np.sin(2*x), 'c-', linewidth=2)
ax4.set_title('Lateral Izquierda')
ax4.grid(True, alpha=0.3)
ax5 = fig.add_subplot(gs[1:3, 3])
ax5.plot(x, np.cos(2*x), 'y-', linewidth=2)
ax5.set_title('Lateral Derecha')
ax5.grid(True, alpha=0.3)
ax6 = fig.add_subplot(gs[3, :2])
ax6.plot(x, np.sin(x) * np.cos(x), 'k-', linewidth=2)
ax6.set_title('Inferior Izquierda')
ax6.grid(True, alpha=0.3)
ax7 = fig.add_subplot(gs[3, 2:])
ax7.plot(x, np.sin(x)**2, 'orange', linewidth=2)
ax7.set_title('Inferior Derecha')
ax7.grid(True, alpha=0.3)
plt.show()Ejes Compartidos
Comparte ejes entre subplots para una mejor comparación visual.
Compartir Ejes X
import matplotlib.pyplot as plt
import numpy as np
# Datos
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)
# Crear subplots con eje X compartido
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(10, 8), sharex=True)
# Graficar en cada subplot
ax1.plot(x, y1, 'b-', linewidth=2)
ax1.set_title('sin(x)')
ax1.grid(True, alpha=0.3)
ax1.set_ylabel('Amplitud')
ax2.plot(x, y2, 'r-', linewidth=2)
ax2.set_title('cos(x)')
ax2.grid(True, alpha=0.3)
ax2.set_ylabel('Amplitud')
ax3.plot(x, y3, 'g-', linewidth=2)
ax3.set_title('sin(x + π/4)')
ax3.grid(True, alpha=0.3)
ax3.set_xlabel('x')
ax3.set_ylabel('Amplitud')
plt.tight_layout()
plt.show()Compartir Ambos Ejes
import matplotlib.pyplot as plt
import numpy as np
# Generar datos relacionados
np.random.seed(42)
x = np.linspace(0, 10, 50)
y1 = np.sin(x) + np.random.normal(0, 0.1, len(x))
y2 = np.cos(x) + np.random.normal(0, 0.1, len(x))
# Crear subplots con ambos ejes compartidos
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(12, 8), sharex=True, sharey=True)
# Scatter plots
ax1.scatter(x, y1, alpha=0.7, color='blue')
ax1.set_title('Datos 1')
ax1.grid(True, alpha=0.3)
ax2.scatter(x, y2, alpha=0.7, color='red')
ax2.set_title('Datos 2')
ax2.grid(True, alpha=0.3)
# Histogramas
ax3.hist(y1, bins=15, alpha=0.7, color='blue', edgecolor='black')
ax3.set_title('Histograma 1')
ax3.set_xlabel('Valor')
ax3.set_ylabel('Frecuencia')
ax3.grid(True, alpha=0.3)
ax4.hist(y2, bins=15, alpha=0.7, color='red', edgecolor='black')
ax4.set_title('Histograma 2')
ax4.set_xlabel('Valor')
ax4.set_ylabel('Frecuencia')
ax4.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Ejes Compartidos con Diferentes Escalas
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.exp(x/5) # Escala diferente
# Crear subplots con eje X compartido pero Y independiente
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8), sharex=True)
# Primer gráfico
ax1.plot(x, y1, 'b-', linewidth=2)
ax1.set_title('Función Trigonométrica')
ax1.set_ylabel('sin(x)')
ax1.grid(True, alpha=0.3)
ax1.set_ylim(-1.5, 1.5)
# Segundo gráfico
ax2.plot(x, y2, 'r-', linewidth=2)
ax2.set_title('Función Exponencial')
ax2.set_xlabel('x')
ax2.set_ylabel('exp(x/5)')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 3)
plt.tight_layout()
plt.show()Subplots Anidados
Crea subplots dentro de otros subplots para layouts aún más complejos.
Subplot Dentro de Subplot
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
fig = plt.figure(figsize=(14, 10))
# GridSpec principal
gs = gridspec.GridSpec(2, 2, figure=fig)
# Subplot principal
ax_main = fig.add_subplot(gs[0, :])
x = np.linspace(0, 10, 100)
ax_main.plot(x, np.sin(x), 'b-', linewidth=2)
ax_main.set_title('Gráfico Principal')
ax_main.grid(True, alpha=0.3)
# Área para subplots anidados
gs_nested = gridspec.GridSpecFromSubplotSpec(2, 2, subplot_spec=gs[1, :], wspace=0.3, hspace=0.3)
# Subplots anidados
for i in range(2):
for j in range(2):
ax = fig.add_subplot(gs_nested[i, j])
y = np.sin(x + (i*2 + j) * np.pi/4)
ax.plot(x, y, linewidth=2, color=f'C{i*2 + j}')
ax.set_title(f'Anidado {i*2 + j + 1}')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Inset Plots
import matplotlib.pyplot as plt
import numpy as np
# Datos principales
x = np.linspace(0, 10, 100)
y = np.sin(x) * np.exp(-x/10)
# Crear gráfico principal
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x, y, 'b-', linewidth=2)
ax.set_title('Gráfico Principal con Inset')
ax.grid(True, alpha=0.3)
# Crear inset (gráfico pequeño dentro del principal)
ax_inset = fig.add_axes([0.65, 0.65, 0.25, 0.25]) # [left, bottom, width, height]
# Datos para el inset (zoom de una región)
x_zoom = np.linspace(2, 4, 100)
y_zoom = np.sin(x_zoom) * np.exp(-x_zoom/10)
ax_inset.plot(x_zoom, y_zoom, 'r-', linewidth=2)
ax_inset.set_title('Zoom', fontsize=10)
ax_inset.grid(True, alpha=0.3)
# Marcar la región del zoom en el gráfico principal
ax.axvspan(2, 4, alpha=0.2, color='red', label='Región del zoom')
ax.legend()
plt.show()Control de Espaciado
Gestiona el espaciado entre subplots para layouts perfectos.
Ajuste Manual de Espaciado
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
x = np.linspace(0, 10, 100)
for i, ax in enumerate(axes.flat):
y = np.sin(x + i * np.pi/4)
ax.plot(x, y, linewidth=2, color=f'C{i}')
ax.set_title(f'Subplot {i+1}')
ax.grid(True, alpha=0.3)
# Ajustar espaciado manualmente
plt.subplots_adjust(left=0.1, # Margen izquierdo
right=0.9, # Margen derecho
bottom=0.1, # Margen inferior
top=0.9, # Margen superior
wspace=0.3, # Espaciado horizontal
hspace=0.4) # Espaciado vertical
plt.show()tight_layout() Avanzado
import matplotlib.pyplot as plt
import numpy as np
fig, axes = plt.subplots(3, 2, figsize=(12, 10))
x = np.linspace(0, 10, 100)
for i, ax in enumerate(axes.flat):
y = np.sin(x + i * np.pi/6)
ax.plot(x, y, linewidth=2, color=f'C{i}')
ax.set_title(f'Función {i+1}', fontsize=12, fontweight='bold')
ax.grid(True, alpha=0.3)
# tight_layout con parámetros personalizados
plt.tight_layout(pad=2.0, # Padding general
h_pad=3.0, # Padding horizontal
w_pad=2.0, # Padding vertical
rect=[0.05, 0.05, 0.95, 0.95]) # Área utilizable [left, bottom, right, top]
plt.show()Layouts Personalizados
Crea diseños únicos que se adapten a tus necesidades específicas.
Layout Asimétrico
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
fig = plt.figure(figsize=(14, 10))
# GridSpec asimétrico
gs = gridspec.GridSpec(3, 4, figure=fig, wspace=0.4, hspace=0.4)
x = np.linspace(0, 10, 100)
# Subplot grande (ocupa 2 filas y 3 columnas)
ax_big = fig.add_subplot(gs[:2, :3])
ax_big.plot(x, np.sin(x), 'b-', linewidth=3)
ax_big.set_title('Gráfico Principal (2x3)', fontsize=14, fontweight='bold')
ax_big.grid(True, alpha=0.3)
# Subplot vertical (2 filas, 1 columna)
ax_vertical = fig.add_subplot(gs[:2, 3])
y_vertical = np.cos(x)
ax_vertical.plot(y_vertical, x, 'r-', linewidth=2)
ax_vertical.set_title('Vertical', fontsize=12)
ax_vertical.grid(True, alpha=0.3)
# Subplot horizontal (1 fila, 4 columnas)
ax_horizontal = fig.add_subplot(gs[2, :])
ax_horizontal.plot(x, np.sin(x) * np.cos(x), 'g-', linewidth=2)
ax_horizontal.set_title('Horizontal (1x4)', fontsize=12)
ax_horizontal.grid(True, alpha=0.3)
plt.show()Layout en Forma de L
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
fig = plt.figure(figsize=(12, 8))
# GridSpec para layout en L
gs = gridspec.GridSpec(3, 3, figure=fig, wspace=0.3, hspace=0.3)
x = np.linspace(0, 10, 100)
# Subplot grande (ocupa esquina superior izquierda)
ax_main = fig.add_subplot(gs[:2, :2])
ax_main.plot(x, np.sin(x), 'b-', linewidth=3)
ax_main.set_title('Principal', fontsize=14, fontweight='bold')
ax_main.grid(True, alpha=0.3)
# Subplot derecho superior
ax_top_right = fig.add_subplot(gs[0, 2])
ax_top_right.plot(x, np.cos(x), 'r-', linewidth=2)
ax_top_right.set_title('Superior Der.', fontsize=10)
ax_top_right.grid(True, alpha=0.3)
# Subplot inferior derecho
ax_bottom_right = fig.add_subplot(gs[1:, 2])
ax_bottom_right.plot(x, np.sin(x + np.pi/4), 'g-', linewidth=2)
ax_bottom_right.set_title('Inferior Der.', fontsize=10)
ax_bottom_right.grid(True, alpha=0.3)
# Subplot inferior izquierdo
ax_bottom_left = fig.add_subplot(gs[2, :2])
ax_bottom_left.plot(x, np.cos(x + np.pi/4), 'm-', linewidth=2)
ax_bottom_left.set_title('Inferior Izq.', fontsize=10)
ax_bottom_left.grid(True, alpha=0.3)
plt.show()Casos de Uso Avanzados
Dashboard de Análisis de Datos
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
# Simular datos de análisis
np.random.seed(42)
x = np.linspace(0, 100, 100)
ventas = 1000 + 500 * np.sin(x/10) + np.random.normal(0, 100, 100)
clientes = 50 + 20 * np.cos(x/15) + np.random.normal(0, 5, 100)
satisfaccion = 4.0 + 0.5 * np.sin(x/20) + np.random.normal(0, 0.2, 100)
fig = plt.figure(figsize=(16, 12))
# GridSpec para dashboard
gs = gridspec.GridSpec(4, 4, figure=fig, wspace=0.4, hspace=0.4)
# Gráfico principal de tendencias
ax_main = fig.add_subplot(gs[:2, :3])
ax_main.plot(x, ventas, 'b-', linewidth=2, label='Ventas')
ax_main.set_title('Tendencia de Ventas', fontsize=16, fontweight='bold')
ax_main.set_xlabel('Tiempo (días)')
ax_main.set_ylabel('Ventas ($)')
ax_main.grid(True, alpha=0.3)
ax_main.legend()
# Gráfico de clientes
ax_clients = fig.add_subplot(gs[:2, 3])
ax_clients.plot(x, clientes, 'g-', linewidth=2)
ax_clients.set_title('Clientes', fontsize=12)
ax_clients.set_xlabel('Tiempo')
ax_clients.set_ylabel('N° Clientes')
ax_clients.grid(True, alpha=0.3)
# Histograma de ventas
ax_hist = fig.add_subplot(gs[2, :2])
ax_hist.hist(ventas, bins=20, alpha=0.7, color='blue', edgecolor='black')
ax_hist.set_title('Distribución de Ventas', fontsize=12)
ax_hist.set_xlabel('Ventas ($)')
ax_hist.set_ylabel('Frecuencia')
ax_hist.grid(True, alpha=0.3)
# Gráfico de satisfacción
ax_satisfaction = fig.add_subplot(gs[2, 2:])
ax_satisfaction.plot(x, satisfaccion, 'r-', linewidth=2)
ax_satisfaction.set_title('Satisfacción del Cliente', fontsize=12)
ax_satisfaction.set_xlabel('Tiempo')
ax_satisfaction.set_ylabel('Satisfacción (1-5)')
ax_satisfaction.set_ylim(2, 5)
ax_satisfaction.grid(True, alpha=0.3)
# Scatter plot: ventas vs clientes
ax_scatter = fig.add_subplot(gs[3, :2])
ax_scatter.scatter(ventas, clientes, alpha=0.6, c=satisfaccion, cmap='viridis')
ax_scatter.set_title('Relación Ventas-Clientes', fontsize=12)
ax_scatter.set_xlabel('Ventas ($)')
ax_scatter.set_ylabel('N° Clientes')
ax_scatter.grid(True, alpha=0.3)
# Estadísticas resumen
ax_stats = fig.add_subplot(gs[3, 2:])
ax_stats.axis('off') # Ocultar ejes
# Agregar texto con estadísticas
stats_text = ".1f"".1f"".2f"f"""
📊 Estadísticas del Período:
Ventas Totales: ${ventas.sum():,.0f}
Promedio Diario: ${ventas.mean():,.0f}
Máximo: ${ventas.max():,.0f}
Mínimo: ${ventas.min():,.0f}
Clientes Totales: {clientes.sum():,.0f}
Satisfacción Promedio: {satisfaccion.mean():.2f}/5.0
Correlación V-C: {np.corrcoef(ventas, clientes)[0,1]:.3f}
"""
ax_stats.text(0.05, 0.95, stats_text, transform=ax_stats.transAxes,
fontsize=10, verticalalignment='top', fontfamily='monospace',
bbox=dict(boxstyle='round,pad=0.5', facecolor='lightgray', alpha=0.8))
plt.show()Visualización Científica Compleja
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
# Simular datos científicos
x = np.linspace(0, 10, 1000)
frecuencia = 2 * np.pi * 1 # 1 Hz
senal = np.sin(frecuencia * x) * np.exp(-x/5) + 0.1 * np.random.randn(len(x))
fig = plt.figure(figsize=(16, 12))
# GridSpec para análisis científico
gs = gridspec.GridSpec(4, 4, figure=fig, wspace=0.4, hspace=0.5)
# Señal temporal
ax_signal = fig.add_subplot(gs[0, :3])
ax_signal.plot(x, senal, 'b-', linewidth=1, alpha=0.8)
ax_signal.set_title('Señal Temporal', fontsize=14, fontweight='bold')
ax_signal.set_xlabel('Tiempo (s)')
ax_signal.set_ylabel('Amplitud')
ax_signal.grid(True, alpha=0.3)
# Histograma de amplitud
ax_hist = fig.add_subplot(gs[0, 3])
ax_hist.hist(senal, bins=30, orientation='horizontal', alpha=0.7, color='blue', edgecolor='black')
ax_hist.set_title('Histograma', fontsize=12)
ax_hist.set_ylabel('Amplitud')
ax_hist.grid(True, alpha=0.3)
# Espectro de frecuencia
ax_spectrum = fig.add_subplot(gs[1, :2])
frecuencias = np.fft.fftfreq(len(x), x[1] - x[0])
espectro = np.abs(np.fft.fft(senal))
ax_spectrum.plot(frecuencias[:len(frecuencias)//2], espectro[:len(espectro)//2], 'r-', linewidth=2)
ax_spectrum.set_title('Espectro de Frecuencia', fontsize=12)
ax_spectrum.set_xlabel('Frecuencia (Hz)')
ax_spectrum.set_ylabel('Magnitud')
ax_spectrum.grid(True, alpha=0.3)
# Diagrama de fase
ax_phase = fig.add_subplot(gs[1, 2:])
fase = np.angle(np.fft.fft(senal))
ax_phase.plot(frecuencias[:len(frecuencias)//2], fase[:len(fase)//2], 'g-', linewidth=2)
ax_phase.set_title('Diagrama de Fase', fontsize=12)
ax_phase.set_xlabel('Frecuencia (Hz)')
ax_phase.set_ylabel('Fase (radianes)')
ax_phase.grid(True, alpha=0.3)
# Análisis estadístico
ax_stats = fig.add_subplot(gs[2:, :2])
ax_stats.axis('off')
# Calcular estadísticas
media = np.mean(senal)
desvio = np.std(senal)
maximo = np.max(senal)
minimo = np.min(senal)
rms = np.sqrt(np.mean(senal**2))
stats_text = ".4f"".4f"".4f"".4f"".4f"f"""
📈 Análisis Estadístico:
Media: {media:.4f}
Desvío Estándar: {desvio:.4f}
Valor Máximo: {maximo:.4f}
Valor Mínimo: {minimo:.4f}
RMS: {rms:.4f}
Coeficiente de Variación: {desvio/abs(media):.4f}
Rango: {maximo - minimo:.4f}
"""
ax_stats.text(0.05, 0.95, stats_text, transform=ax_stats.transAxes,
fontsize=11, verticalalignment='top', fontfamily='monospace',
bbox=dict(boxstyle='round,pad=0.5', facecolor='lightyellow', alpha=0.9))
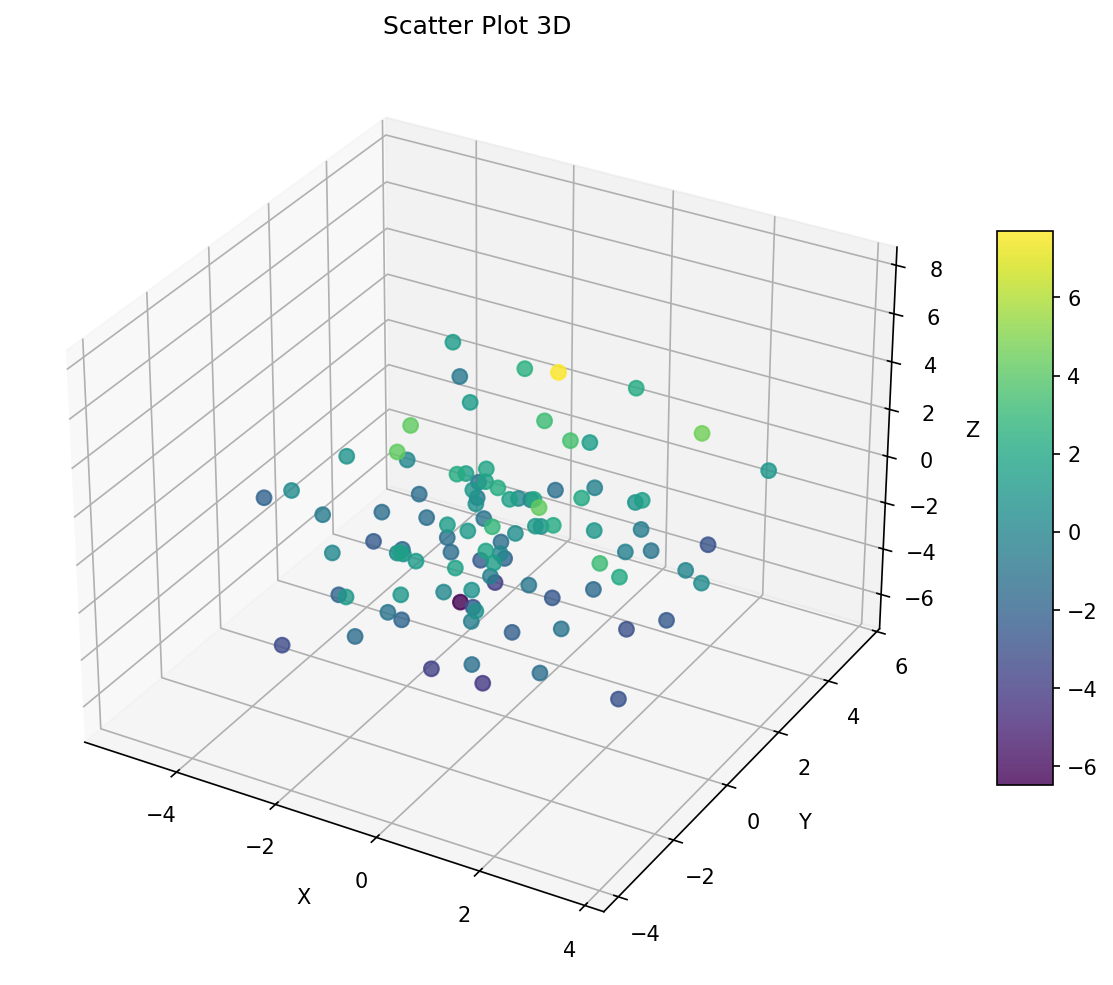
# Gráfico 3D de densidad (simplificado)
ax_3d = fig.add_subplot(gs[2:, 2:], projection='3d')
X, Y = np.meshgrid(x[::10], np.linspace(-2, 2, 50))
Z = np.exp(-(X-5)**2 - Y**2) * np.sin(2*np.pi*X/10)
surf = ax_3d.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax_3d.set_title('Densidad 3D', fontsize=12)
ax_3d.set_xlabel('Tiempo')
ax_3d.set_ylabel('Amplitud')
ax_3d.set_zlabel('Densidad')
plt.colorbar(surf, ax=ax_3d, shrink=0.6, aspect=10)
plt.show()¡Has dominado la creación de layouts complejos con subplots en Matplotlib! Ahora puedes crear visualizaciones profesionales con múltiples gráficos organizados de manera efectiva.
En el próximo tutorial aprenderás sobre Gráficos Avanzados como histogramas, mapas de calor y visualizaciones estadísticas complejas.


No hay comentarios aún
Sé el primero en comentar este tutorial.