Matplotlib

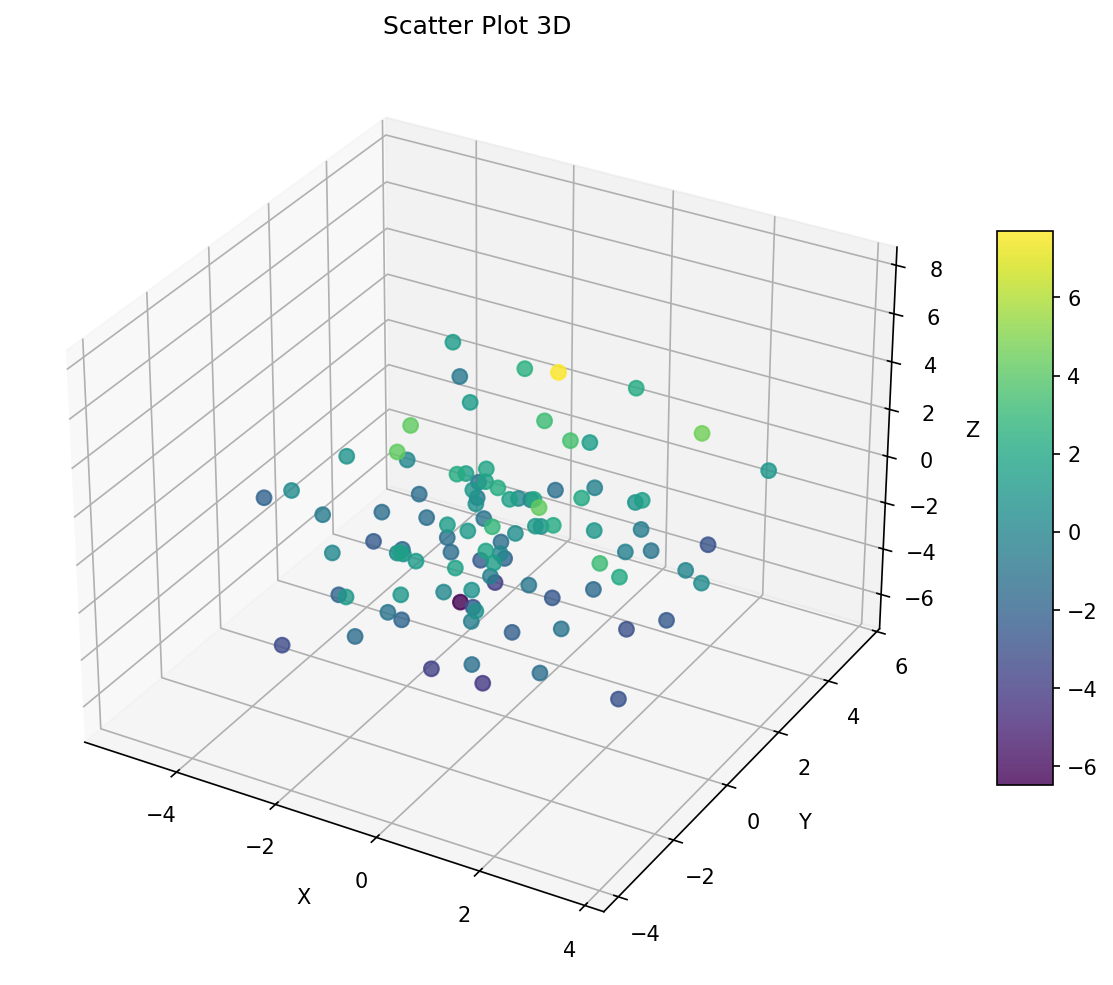
Gráficos 3D con Matplotlib: Visualización Tridimensional

José Elías Romero Guanipa

01 Sep 2025

Aprende a crear gráficos 3D impactantes con Matplotlib: superficies, dispersión 3D, líneas 3D, barras 3D y animaciones tridimensionales.

matplotlib python visualizacion 3d superficies +2 más

¡Explora el fascinante mundo de la visualización 3D con Matplotlib! En este tutorial aprenderás a crear gráficos tridimensionales impactantes que te permitirán visualizar datos complejos desde nuevas perspectivas.

Objetivo: Dominar la creación de visualizaciones 3D en Matplotlib, incluyendo superficies, gráficos de dispersión tridimensionales, líneas 3D, barras 3D y animaciones.

Introducción a Gráficos 3D

Los gráficos 3D permiten visualizar datos en tres dimensiones, revelando patrones y relaciones que no son evidentes en gráficos 2D.

Ventajas de los Gráficos 3D

Visualización de relaciones complejas: Muestra interacciones entre tres variables
Análisis espacial: Ideal para datos con componentes espaciales
Presentaciones impactantes: Gráficos más atractivos para audiencias
Análisis científico: Común en física, química, biología y geociencias
Modelado: Visualización de funciones matemáticas complejas

Limitaciones

Complejidad de interpretación: Puede ser difícil de leer correctamente
Distorsión visual: La perspectiva puede engañar sobre magnitudes
Rendimiento: Más lento que gráficos 2D
Impresión: Difícil de imprimir en blanco y negro

Configuración del Entorno 3D

Aprende los fundamentos para configurar tu entorno de trabajo 3D en Matplotlib. Esta sección cubre la importación de módulos necesarios, creación de figuras 3D básicas y configuración avanzada de ejes, vistas y parámetros visuales que servirán como base para todos los gráficos tridimensionales que crearás.

Para crear gráficos 3D, necesitamos importar el módulo mpl_toolkits.mplot3d.

Configuración Básica

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear figura con ejes 3D
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Configurar etiquetas
ax.set_xlabel('Eje X')
ax.set_ylabel('Eje Y')
ax.set_zlabel('Eje Z')
ax.set_title('Gráfico 3D Básico')

plt.show()

Configuración 3D Básica Fig. 2: Configuración básica de un gráfico 3D en Matplotlib

Configuración Avanzada

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Configuración avanzada del entorno 3D
fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# Configurar límites de ejes
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.set_zlim(-5, 5)

# Configurar etiquetas con formato
ax.set_xlabel('Eje X', fontsize=12, fontweight='bold')
ax.set_ylabel('Eje Y', fontsize=12, fontweight='bold')
ax.set_zlabel('Eje Z', fontsize=12, fontweight='bold')
ax.set_title('Configuración Avanzada 3D', fontsize=14, fontweight='bold')

# Configurar vista inicial
ax.view_init(elev=20, azim=45)  # elevación y azimut

# Configurar ticks
ax.set_xticks(np.arange(-5, 6, 1))
ax.set_yticks(np.arange(-5, 6, 1))
ax.set_zticks(np.arange(-5, 6, 1))

# Agregar grid
ax.grid(True, alpha=0.3)

plt.show()

Gráficos de Dispersión 3D

Descubre cómo crear gráficos de dispersión tridimensionales para visualizar la distribución de puntos en el espacio 3D. Aprenderás a representar datos con colores variables, tamaños dinámicos y múltiples grupos, lo que te permitirá identificar patrones y agrupaciones en conjuntos de datos complejos.

Los gráficos de dispersión 3D muestran puntos en el espacio tridimensional.

Scatter 3D Básico

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Generar datos
np.random.seed(42)
n = 100
x = np.random.normal(0, 2, n)
y = np.random.normal(0, 2, n)
z = np.random.normal(0, 2, n)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear scatter plot 3D
scatter = ax.scatter(x, y, z, c=z, cmap='viridis', s=50, alpha=0.8)

# Configurar apariencia
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Gráfico de Dispersión 3D Básico')

# Agregar barra de colores
cbar = plt.colorbar(scatter, shrink=0.6, aspect=10)
cbar.set_label('Valor Z')

plt.show()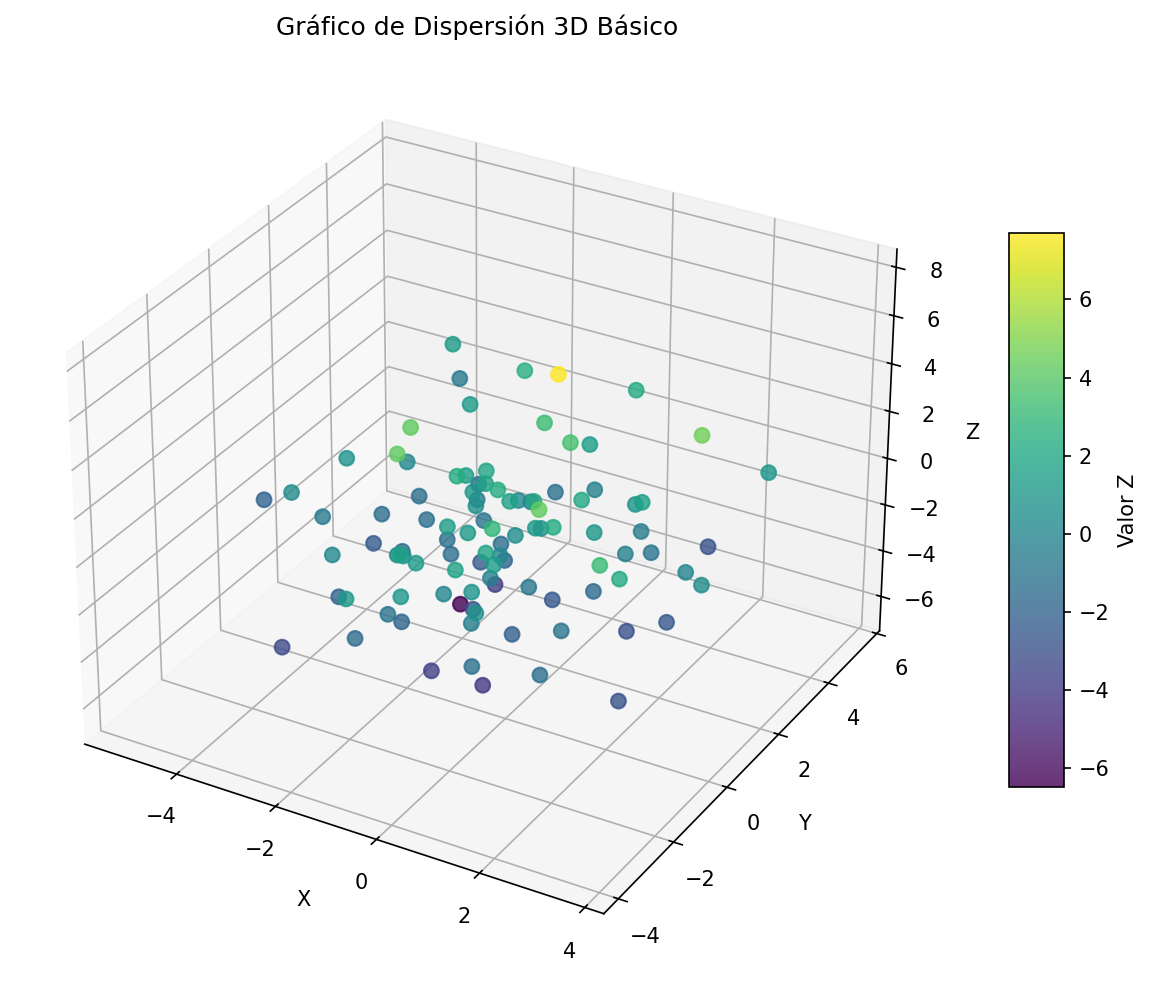

Gráfico de Dispersión 3D Básico Fig. 3: Gráfico de dispersión tridimensional básico con colores

Scatter 3D con Múltiples Grupos

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Generar datos para tres grupos
np.random.seed(42)
n = 50

# Grupo 1
x1 = np.random.normal(0, 1, n)
y1 = np.random.normal(0, 1, n)
z1 = np.random.normal(0, 1, n)

# Grupo 2
x2 = np.random.normal(3, 1, n)
y2 = np.random.normal(3, 1, n)
z2 = np.random.normal(3, 1, n)

# Grupo 3
x3 = np.random.normal(0, 1, n)
y3 = np.random.normal(3, 1, n)
z3 = np.random.normal(1.5, 1, n)

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# Graficar cada grupo con colores diferentes
ax.scatter(x1, y1, z1, c='red', s=60, alpha=0.7, label='Grupo 1')
ax.scatter(x2, y2, z2, c='blue', s=60, alpha=0.7, label='Grupo 2')
ax.scatter(x3, y3, z3, c='green', s=60, alpha=0.7, label='Grupo 3')

# Configurar gráfico
ax.set_xlabel('Variable X')
ax.set_ylabel('Variable Y')
ax.set_zlabel('Variable Z')
ax.set_title('Dispersión 3D con Múltiples Grupos')
ax.legend()

# Configurar vista
ax.view_init(elev=20, azim=45)

plt.show()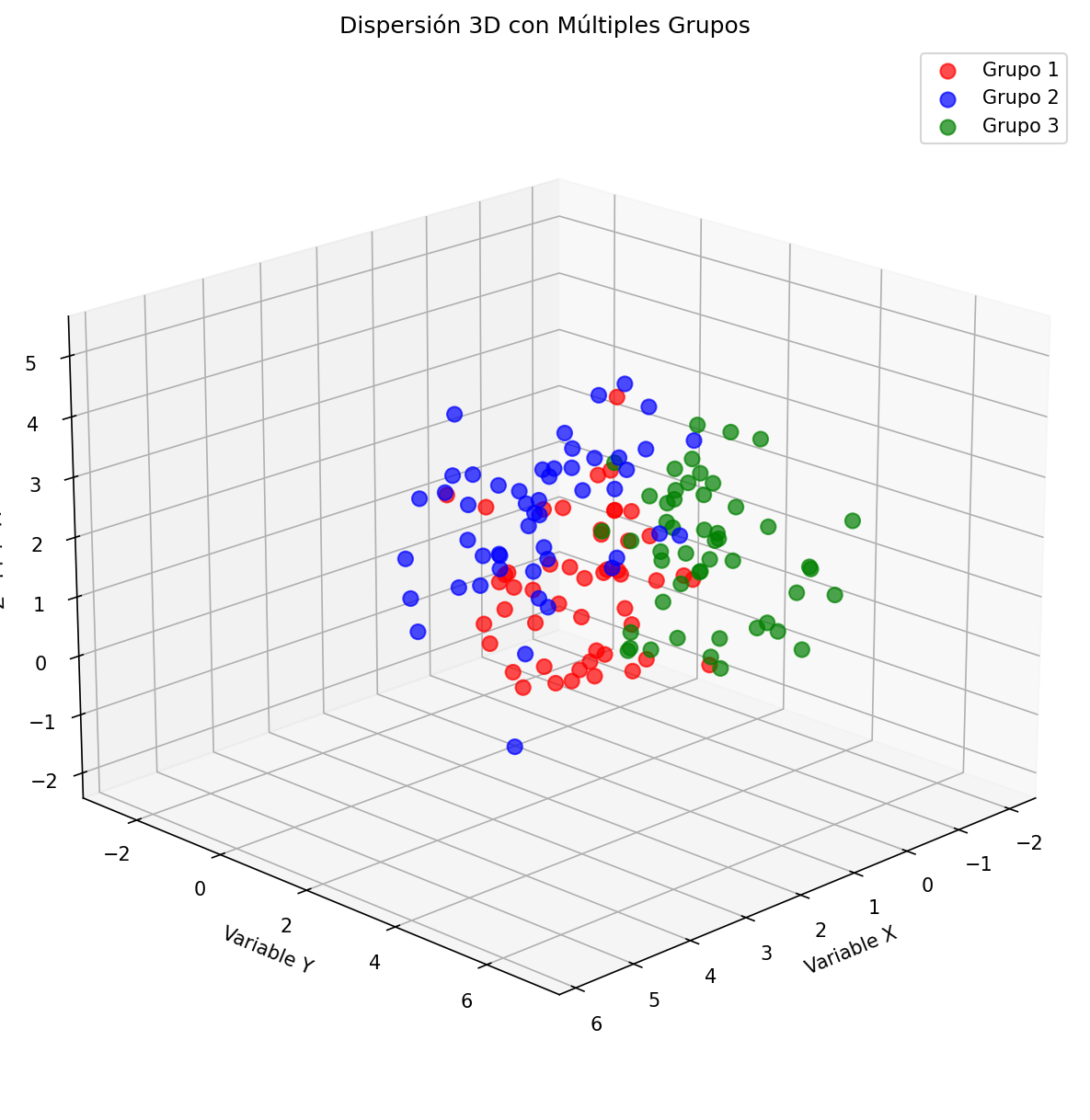

Fig. 4: Gráfico de dispersión 3D con múltiples grupos de colores

Scatter 3D con Tamaño Variable

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Datos con tamaño variable
np.random.seed(42)
n = 200
x = np.random.normal(0, 3, n)
y = np.random.normal(0, 3, n)
z = np.random.normal(0, 3, n)

# Calcular distancias desde el origen para determinar tamaño
distancia = np.sqrt(x**2 + y**2 + z**2)
tamano = 20 + 80 * (distancia / np.max(distancia))  # Tamaño entre 20 y 100

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Scatter con tamaño variable
scatter = ax.scatter(x, y, z, s=tamano, c=distancia, cmap='plasma',
                    alpha=0.6, edgecolors='black', linewidth=0.5)

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Scatter 3D con Tamaño Variable')

# Barra de colores
cbar = plt.colorbar(scatter, shrink=0.6, aspect=10)
cbar.set_label('Distancia al Origen')

# Configurar vista
ax.view_init(elev=25, azim=45)

plt.show()

Scatter plot 3D con colores Fig. 1: Gráfico de dispersión tridimensional con colores variables

Gráficos de Líneas 3D

Explora las técnicas para crear líneas tridimensionales que conectan puntos en el espacio 3D. Aprenderás a generar trayectorias paramétricas, espirales, hélices y formas geométricas complejas, además de combinar múltiples líneas en un mismo gráfico para comparaciones efectivas.

Los gráficos de líneas 3D conectan puntos en el espacio tridimensional.

Líneas 3D Básicas

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Generar datos paramétricos
t = np.linspace(0, 4*np.pi, 100)
x = np.sin(t)
y = np.cos(t)
z = t / (4*np.pi)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Graficar línea 3D
ax.plot(x, y, z, 'b-', linewidth=3, label='Espiral')

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Línea 3D: Espiral')
ax.legend()

# Configurar vista
ax.view_init(elev=20, azim=45)

plt.show()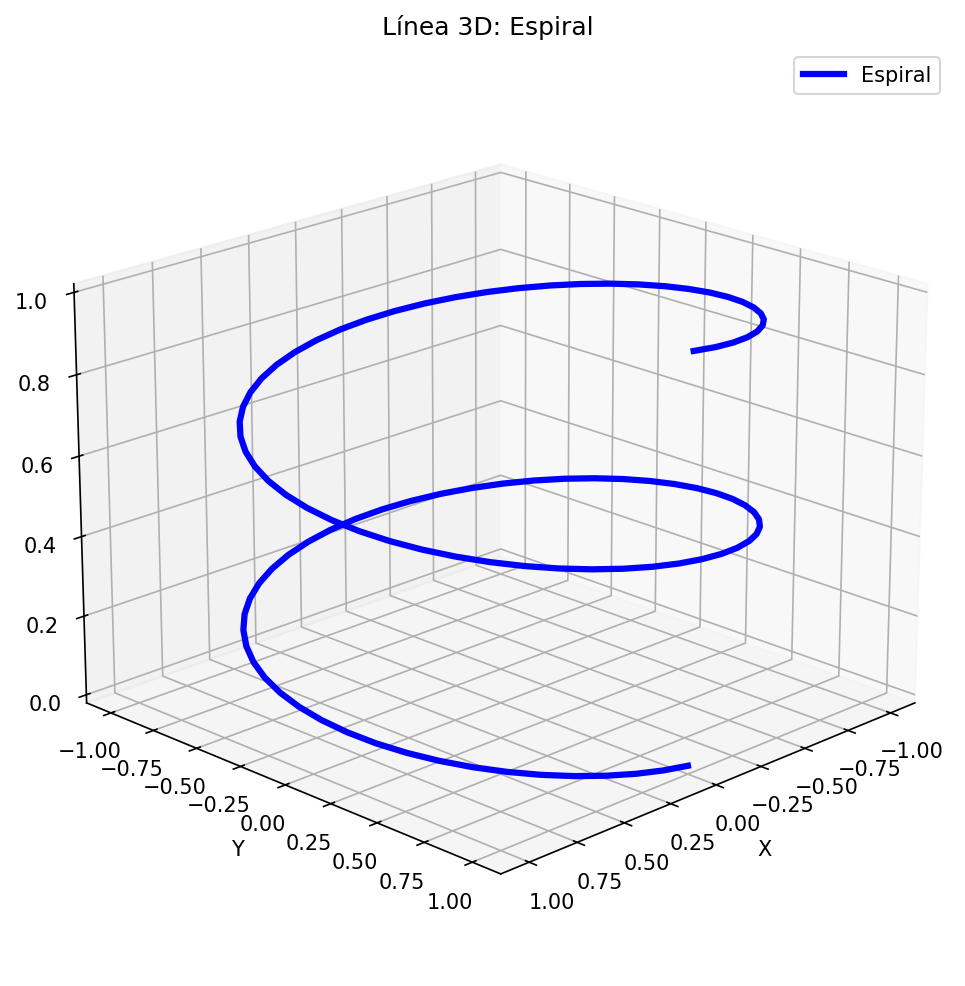

Línea 3D Básica Fig. 5: Gráfico de línea tridimensional en forma de espiral

Múltiples Líneas 3D

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# Espiral ascendente
t1 = np.linspace(0, 6*np.pi, 200)
x1 = np.sin(t1)
y1 = np.cos(t1)
z1 = t1 / (2*np.pi)
ax.plot(x1, y1, z1, 'b-', linewidth=2, label='Espiral Azul')

# Espiral descendente
t2 = np.linspace(0, 6*np.pi, 200)
x2 = np.sin(t2 + np.pi)
y2 = np.cos(t2 + np.pi)
z2 = 3 - t2 / (2*np.pi)
ax.plot(x2, y2, z2, 'r-', linewidth=2, label='Espiral Roja')

# Círculo en plano XY
theta = np.linspace(0, 2*np.pi, 100)
x3 = 2 * np.cos(theta)
y3 = 2 * np.sin(theta)
z3 = np.ones_like(theta) * 1.5
ax.plot(x3, y3, z3, 'g-', linewidth=3, label='Círculo XY')

# Círculo en plano XZ
x4 = 2 * np.cos(theta)
y4 = np.ones_like(theta) * 0
z4 = 2 * np.sin(theta) + 1.5
ax.plot(x4, y4, z4, 'm-', linewidth=3, label='Círculo XZ')

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Múltiples Líneas 3D')
ax.legend()

# Configurar límites
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_zlim(0, 3)

# Configurar vista
ax.view_init(elev=25, azim=45)

plt.show()

Trayectorias 3D

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Simular trayectoria de una partícula
np.random.seed(42)
n = 1000
t = np.linspace(0, 10, n)

# Movimiento helicoidal con ruido
x = np.sin(t) + 0.1 * np.random.randn(n)
y = np.cos(t) + 0.1 * np.random.randn(n)
z = t / 3 + 0.05 * np.random.randn(n)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Graficar trayectoria
ax.plot(x, y, z, 'b-', linewidth=1, alpha=0.8, label='Trayectoria')

# Marcar puntos inicial y final
ax.scatter(x[0], y[0], z[0], c='green', s=100, marker='o', label='Inicio')
ax.scatter(x[-1], y[-1], z[-1], c='red', s=100, marker='X', label='Fin')

# Configurar gráfico
ax.set_xlabel('Posición X')
ax.set_ylabel('Posición Y')
ax.set_zlabel('Posición Z')
ax.set_title('Trayectoria 3D de una Partícula')
ax.legend()

# Configurar vista
ax.view_init(elev=20, azim=45)

plt.show()

Superficies 3D

Domina la creación de superficies tridimensionales para representar funciones matemáticas de dos variables. Esta sección te enseñará a generar superficies continuas, trabajar con ecuaciones paramétricas y crear visualizaciones de formas geométricas complejas como el toro (donut), esenciales para el análisis matemático y científico.

Las superficies 3D muestran funciones de dos variables como una superficie continua.

Superficie Básica

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos para la superficie
x = np.linspace(-5, 5, 50)
y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear superficie
surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8,
                      linewidth=0, antialiased=True)

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Superficie 3D: sin(√(x² + y²))')

# Agregar barra de colores
cbar = plt.colorbar(surf, shrink=0.6, aspect=10)
cbar.set_label('Valor Z')

# Configurar vista
ax.view_init(elev=30, azim=45)

plt.show()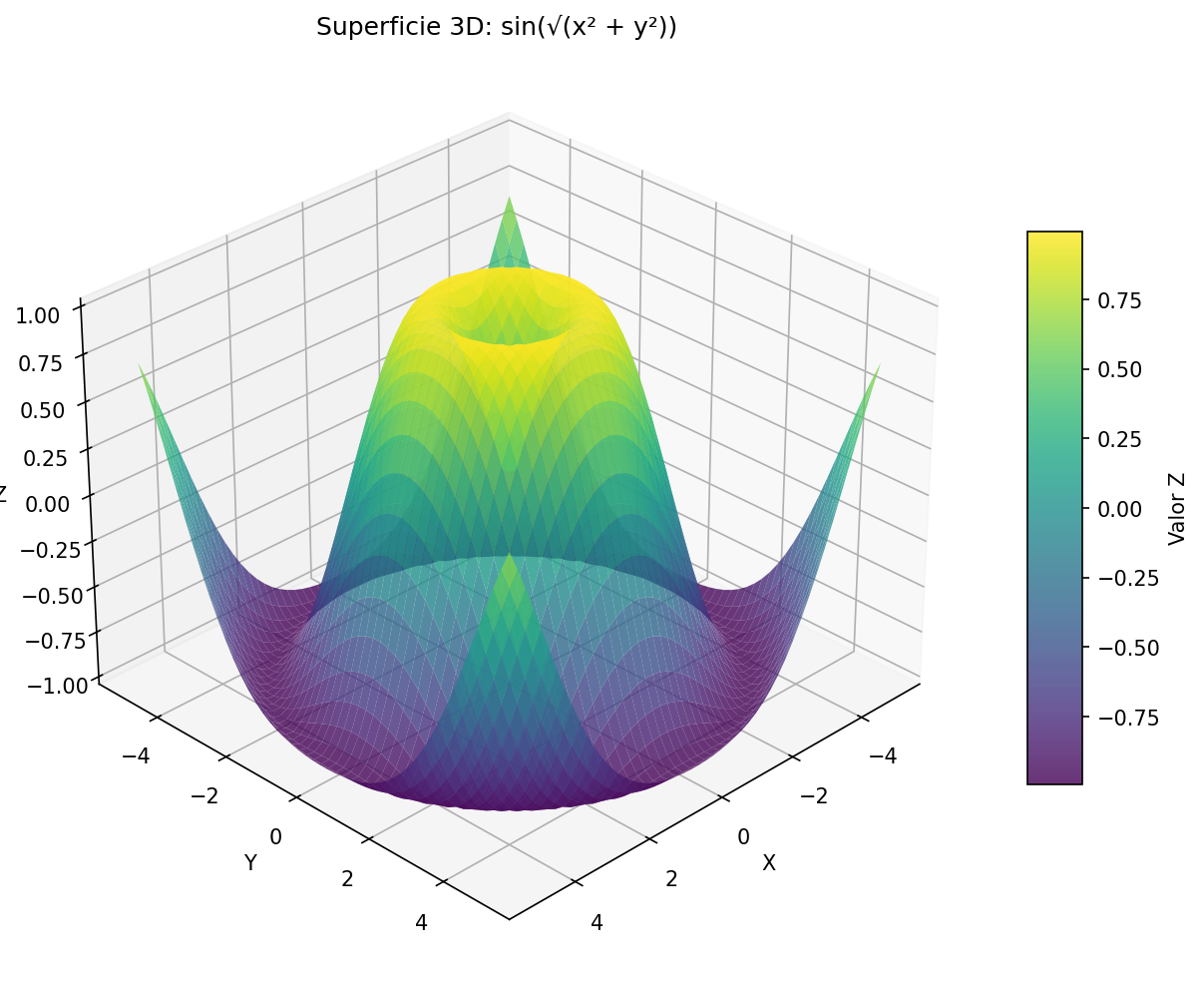

Superficie 3D Básica Fig. 6: Superficie tridimensional de la función sin(√(x² + y²))

Múltiples Superficies

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-3, 3, 40)
y = np.linspace(-3, 3, 40)
X, Y = np.meshgrid(x, y)

# Definir diferentes funciones
Z1 = np.sin(X) * np.cos(Y)
Z2 = X**2 - Y**2
Z3 = np.exp(-(X**2 + Y**2) / 4)

fig = plt.figure(figsize=(16, 12))

# Superficie 1
ax1 = fig.add_subplot(2, 2, 1, projection='3d')
surf1 = ax1.plot_surface(X, Y, Z1, cmap='viridis', alpha=0.8)
ax1.set_title('sin(x) * cos(y)')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')

# Superficie 2
ax2 = fig.add_subplot(2, 2, 2, projection='3d')
surf2 = ax2.plot_surface(X, Y, Z2, cmap='plasma', alpha=0.8)
ax2.set_title('x² - y²')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')

# Superficie 3
ax3 = fig.add_subplot(2, 2, 3, projection='3d')
surf3 = ax3.plot_surface(X, Y, Z3, cmap='inferno', alpha=0.8)
ax3.set_title('exp(-(x² + y²)/4)')
ax3.set_xlabel('X')
ax3.set_ylabel('Y')
ax3.set_zlabel('Z')

# Comparación de contornos
ax4 = fig.add_subplot(2, 2, 4)
cs = ax4.contourf(X, Y, Z1, levels=20, cmap='viridis')
ax4.set_title('Contorno 2D de la primera superficie')
ax4.set_xlabel('X')
ax4.set_ylabel('Y')
plt.colorbar(cs, ax=ax4, shrink=0.8)

plt.tight_layout()
plt.show()

Superficies Paramétricas

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Parámetros para superficie paramétrica (torus)
u = np.linspace(0, 2*np.pi, 50)
v = np.linspace(0, 2*np.pi, 50)
U, V = np.meshgrid(u, v)

# Radio mayor y menor del torus
R = 3
r = 1

# Ecuaciones paramétricas del torus
X = (R + r * np.cos(V)) * np.cos(U)
Y = (R + r * np.cos(V)) * np.sin(U)
Z = r * np.sin(V)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear superficie paramétrica
surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8,
                      linewidth=0, antialiased=True)

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Superficie Paramétrica: Toro (Torus)')

# Configurar límites para vista simétrica
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.set_zlim(-2, 2)

# Configurar vista
ax.view_init(elev=20, azim=45)

plt.show()

Gráficos de Alambre (Wireframe)

Aprende a crear gráficos de alambre (wireframe) que muestran la estructura esquelética de las superficies sin relleno. Esta técnica es útil para visualizar la topología de funciones complejas y comparar diferentes tipos de representación visual, desde superficies sólidas hasta estructuras de malla.

Los gráficos de alambre muestran la estructura de una superficie sin rellenar.

Wireframe Básico

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-5, 5, 30)
y = np.linspace(-5, 5, 30)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear wireframe
wire = ax.plot_wireframe(X, Y, Z, color='blue', linewidth=1, alpha=0.8)

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Gráfico de Alambre (Wireframe)')

# Configurar vista
ax.view_init(elev=30, azim=45)

plt.show()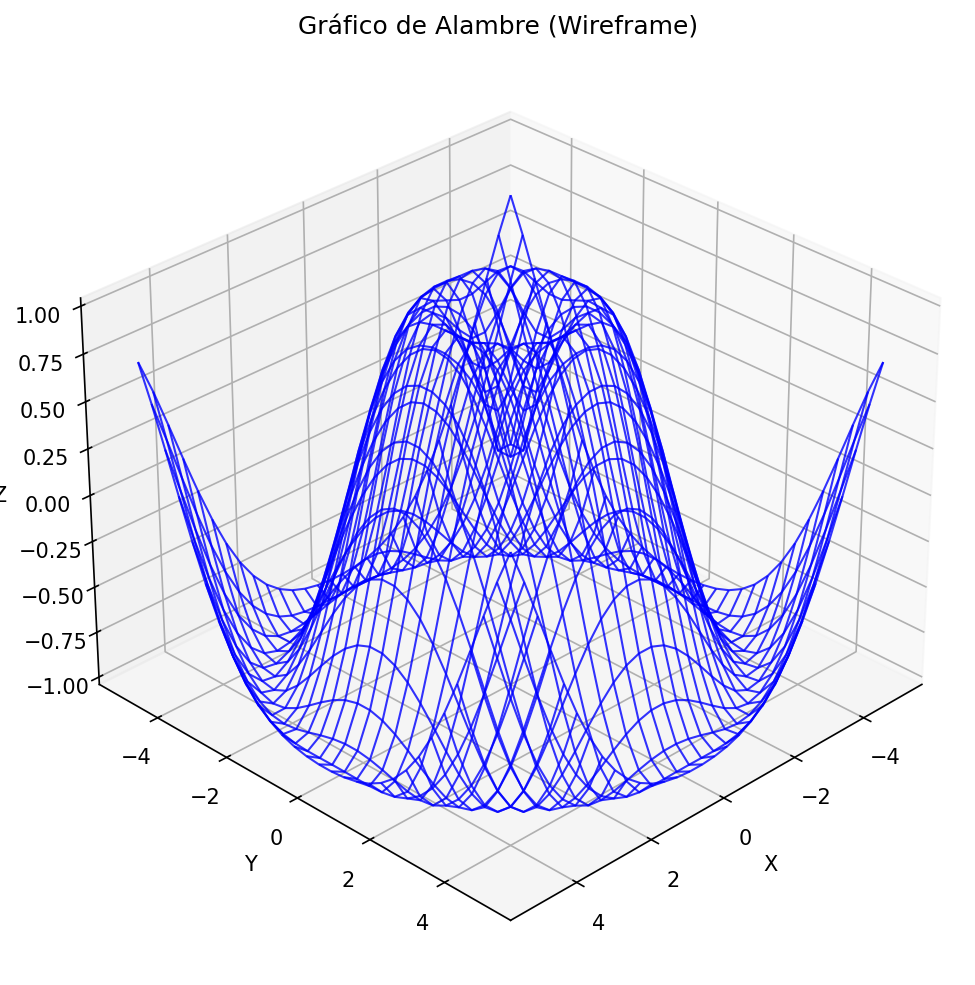

Gráfico de Alambre 3D Fig. 7: Gráfico de alambre (wireframe) tridimensional

Comparación: Superficie vs Wireframe

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-4, 4, 25)
y = np.linspace(-4, 4, 25)
X, Y = np.meshgrid(x, y)
Z = (X**2 + Y**2) / 8

fig = plt.figure(figsize=(16, 8))

# Superficie
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
surf = ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax1.set_title('Superficie 3D')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')

# Wireframe
ax2 = fig.add_subplot(1, 2, 2, projection='3d')
wire = ax2.plot_wireframe(X, Y, Z, color='red', linewidth=1.5, alpha=0.8)
ax2.set_title('Wireframe 3D')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')

# Configurar la misma vista para ambas
for ax in [ax1, ax2]:
    ax.view_init(elev=25, azim=45)
    ax.set_xlim(-4, 4)
    ax.set_ylim(-4, 4)
    ax.set_zlim(0, 4)

plt.tight_layout()
plt.show()

Barras 3D

Descubre cómo representar datos categóricos en formato tridimensional mediante barras 3D. Aprenderás a crear gráficos de barras simples y múltiples series, ideales para comparar valores entre diferentes categorías y períodos de tiempo, con técnicas avanzadas de posicionamiento y visualización.

Las barras 3D muestran datos categóricos en tres dimensiones.

Barras 3D Básicas

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Datos
x = [1, 2, 3, 4, 5]
y = [1, 1, 1, 1, 1]
z = [0, 0, 0, 0, 0]
dx = [0.8, 0.8, 0.8, 0.8, 0.8]
dy = [0.8, 0.8, 0.8, 0.8, 0.8]
dz = [2, 3, 1, 4, 2.5]

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear barras 3D
bars = ax.bar3d(x, y, z, dx, dy, dz, color='skyblue', alpha=0.8, zsort='average')

# Configurar gráfico
ax.set_xlabel('Categoría X')
ax.set_ylabel('Categoría Y')
ax.set_zlabel('Valor')
ax.set_title('Barras 3D Básicas')

# Configurar ticks
ax.set_xticks([1.4, 2.4, 3.4, 4.4, 5.4])
ax.set_xticklabels(['A', 'B', 'C', 'D', 'E'])

plt.show()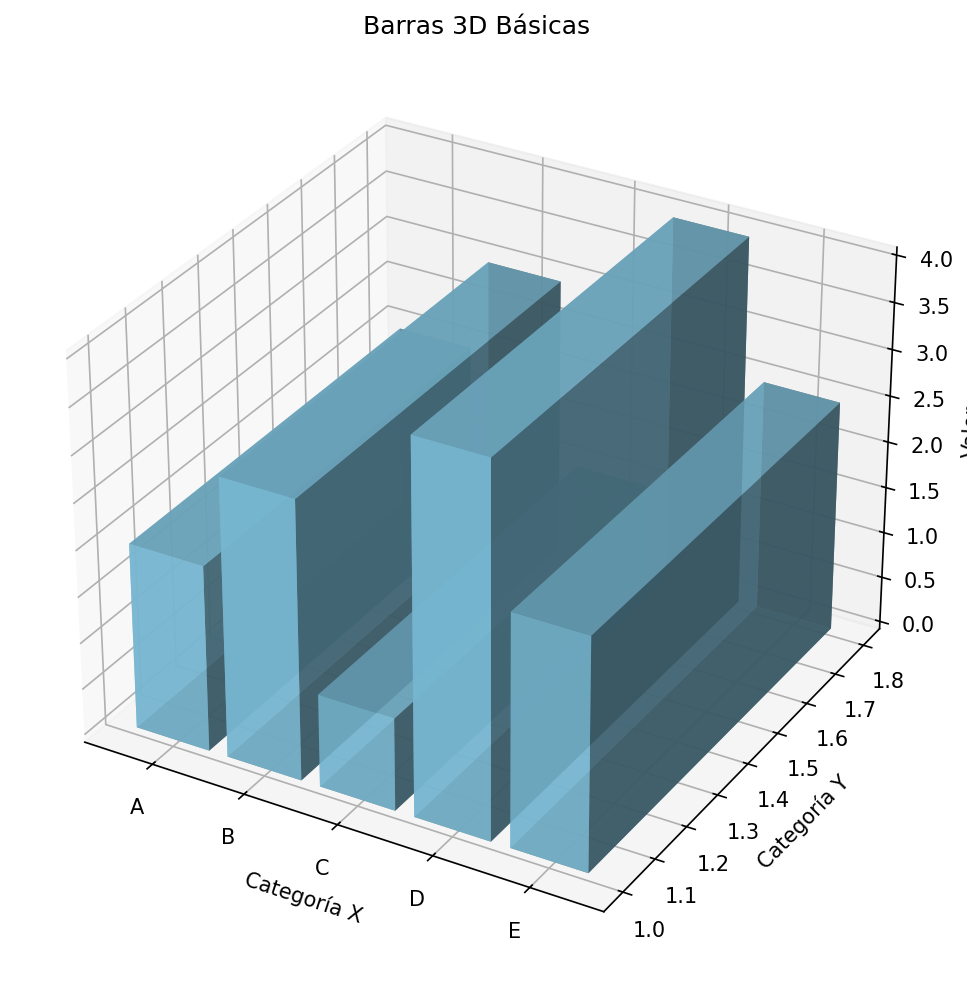

Barras 3D Básicas Fig. 8: Gráfico de barras tridimensional básico

Barras 3D con Múltiples Series

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Datos para múltiples series
categorias_x = ['Producto A', 'Producto B', 'Producto C']
categorias_y = ['Q1', 'Q2', 'Q3', 'Q4']

# Ventas por producto y trimestre
ventas = np.array([
    [120, 150, 180, 200],  # Producto A
    [100, 130, 160, 190],  # Producto B
    [80, 110, 140, 170]    # Producto C
])

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# Colores para cada producto
colores = ['lightblue', 'lightgreen', 'lightcoral']

# Crear barras para cada producto
for i, (producto, color) in enumerate(zip(categorias_x, colores)):
    x_pos = np.arange(len(categorias_y)) + 0.2 * i  # Desplazamiento para separación
    y_pos = np.full_like(x_pos, i)
    z_pos = np.zeros_like(x_pos)

    dx = np.full_like(x_pos, 0.2)  # Ancho de barras
    dy = np.full_like(y_pos, 0.8)  # Profundidad de barras
    dz = ventas[i]

    ax.bar3d(x_pos, y_pos, z_pos, dx, dy, dz, color=color, alpha=0.8,
             label=producto, zsort='average')

# Configurar gráfico
ax.set_xlabel('Trimestre')
ax.set_ylabel('Producto')
ax.set_zlabel('Ventas ($)')
ax.set_title('Ventas por Producto y Trimestre')

# Configurar ticks
ax.set_xticks(np.arange(len(categorias_y)) + 0.3)
ax.set_xticklabels(categorias_y)
ax.set_yticks(np.arange(len(categorias_x)))
ax.set_yticklabels(categorias_x)

# Configurar vista
ax.view_init(elev=20, azim=45)

# Leyenda
ax.legend()

plt.show()

Contornos 3D

Explora las técnicas avanzadas de contornos tridimensionales que combinan información de superficie con líneas de nivel. Aprenderás a crear visualizaciones que muestran isosuperficies, contornos en diferentes planos y representaciones volumétricas, fundamentales para el análisis de campos escalares en física y matemáticas.

Los contornos 3D combinan información de superficie con líneas de nivel.

Contornos 3D Básicos

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# Crear superficie con contornos
surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.6)
cont = ax.contour(X, Y, Z, levels=10, colors='black', linewidths=1, alpha=0.8)

# Configurar gráfico
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Superficie 3D con Contornos')

# Configurar vista
ax.view_init(elev=25, azim=45)

plt.show()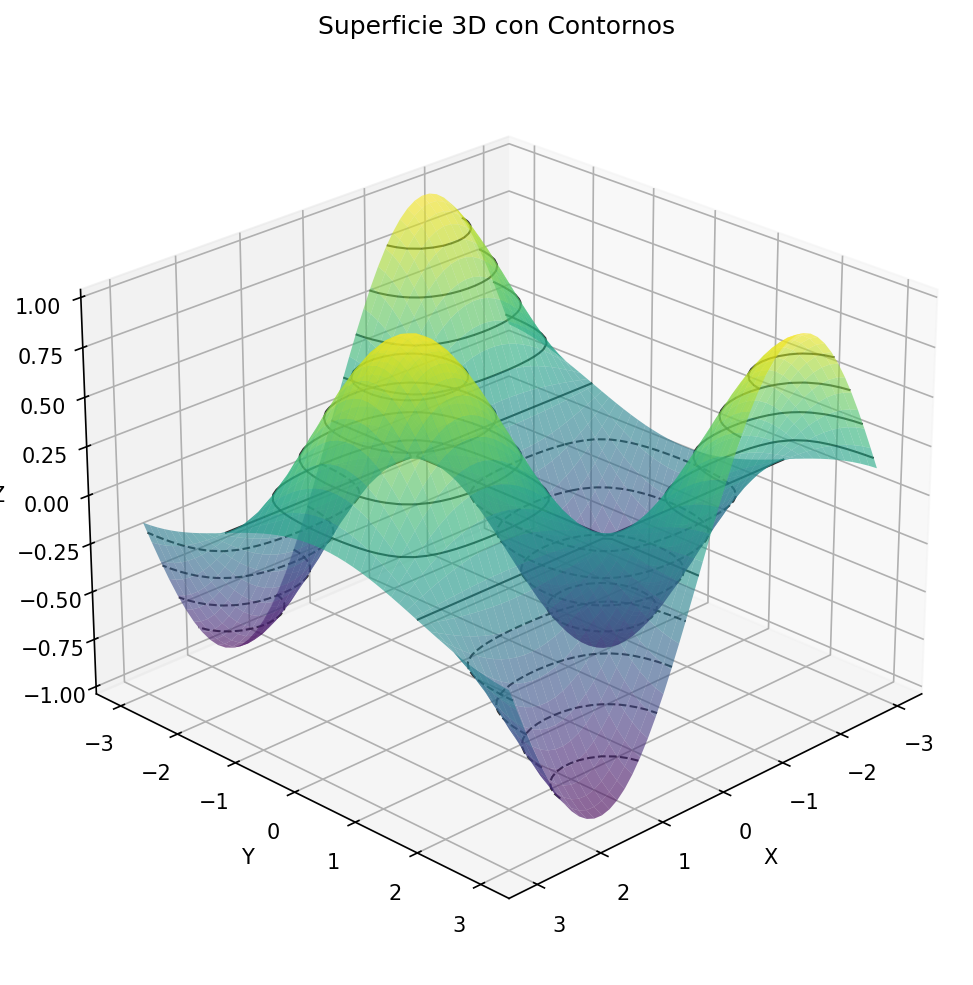

Superficie 3D con Contornos Fig. 9: Superficie tridimensional con líneas de contorno

Contornos en Diferentes Planos

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-4, 4, 40)
y = np.linspace(-4, 4, 40)
z = np.linspace(-4, 4, 40)
X, Y, Z = np.meshgrid(x, y, z)

# Función escalar
F = X**2 + Y**2 + Z**2 - 1  # Esfera

fig = plt.figure(figsize=(16, 12))

# Contornos en plano XY (z=0)
ax1 = fig.add_subplot(2, 2, 1, projection='3d')
cs1 = ax1.contour(X[:, :, 20], Y[:, :, 20], F[:, :, 20], levels=[0],
                  colors='red', linewidths=3)
ax1.set_title('Contorno en Plano XY (z=0)')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')

# Contornos en plano XZ (y=0)
ax2 = fig.add_subplot(2, 2, 2, projection='3d')
cs2 = ax2.contour(X[20, :, :], F[20, :, :], Z[20, :, :], levels=[0],
                  colors='blue', linewidths=3)
ax2.set_title('Contorno en Plano XZ (y=0)')
ax2.set_xlabel('X')
ax2.set_ylabel('F')
ax2.set_zlabel('Z')

# Contornos en plano YZ (x=0)
ax3 = fig.add_subplot(2, 2, 3, projection='3d')
cs3 = ax3.contour(F[:, 20, :], Y[:, 20, :], Z[:, 20, :], levels=[0],
                  colors='green', linewidths=3)
ax3.set_title('Contorno en Plano YZ (x=0)')
ax3.set_xlabel('F')
ax3.set_ylabel('Y')
ax3.set_zlabel('Z')

# Visualización 3D completa
ax4 = fig.add_subplot(2, 2, 4, projection='3d')
# Crear una superficie aproximada de la esfera usando puntos
u = np.linspace(0, 2*np.pi, 20)
v = np.linspace(0, np.pi, 20)
x_sphere = np.outer(np.cos(u), np.sin(v))
y_sphere = np.outer(np.sin(u), np.sin(v))
z_sphere = np.outer(np.ones(np.size(u)), np.cos(v))

ax4.plot_surface(x_sphere, y_sphere, z_sphere, color='cyan', alpha=0.3)
ax4.set_title('Esfera 3D')
ax4.set_xlabel('X')
ax4.set_ylabel('Y')
ax4.set_zlabel('Z')

plt.tight_layout()
plt.show()

Personalización de Gráficos 3D

Domina las técnicas avanzadas de personalización para crear gráficos 3D visualmente impactantes. Esta sección cubre mapas de colores personalizados, efectos de iluminación, configuración de fuentes de luz, estilos de línea, transparencias y otros elementos estéticos que harán que tus visualizaciones destaquen en presentaciones y publicaciones.

Técnicas avanzadas para personalizar la apariencia de gráficos 3D.

Colores y Estilos Personalizados

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-3, 3, 30)
y = np.linspace(-3, 3, 30)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111, projection='3d')

# Superficie con personalización avanzada
surf = ax.plot_surface(X, Y, Z,
                      cmap='plasma',           # Mapa de colores
                      alpha=0.9,               # Transparencia
                      linewidth=0.5,           # Ancho de líneas
                      edgecolors='black',      # Color de bordes
                      antialiased=True,        # Suavizado
                      shade=True,              # Sombreado
                      lightsource=None)        # Fuente de luz personalizada

# Personalizar ejes
ax.set_xlabel('Eje X', fontsize=12, fontweight='bold', color='#2E4057')
ax.set_ylabel('Eje Y', fontsize=12, fontweight='bold', color='#2E4057')
ax.set_zlabel('Eje Z', fontsize=12, fontweight='bold', color='#2E4057')
ax.set_title('Superficie 3D Personalizada', fontsize=14, fontweight='bold')

# Personalizar ticks
ax.tick_params(axis='x', colors='#2E4057', labelsize=10)
ax.tick_params(axis='y', colors='#2E4057', labelsize=10)
ax.tick_params(axis='z', colors='#2E4057', labelsize=10)

# Configurar grid
ax.grid(True, alpha=0.3, color='#BDC3C7')

# Barra de colores personalizada
cbar = plt.colorbar(surf, shrink=0.6, aspect=10, pad=0.1)
cbar.set_label('Valor Z', fontsize=12, fontweight='bold')
cbar.ax.tick_params(labelsize=10)

# Configurar vista
ax.view_init(elev=25, azim=45)

plt.show()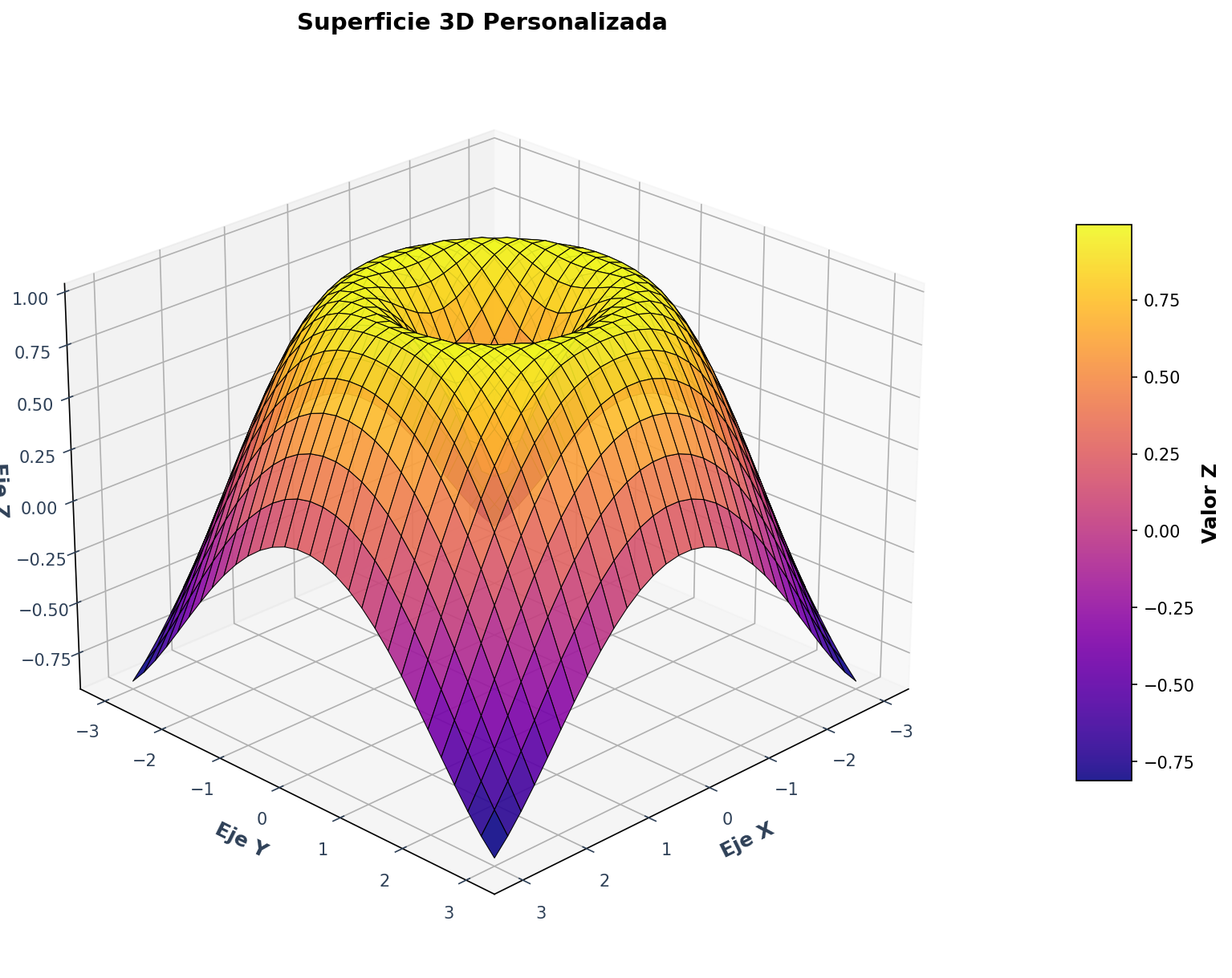

Superficie 3D Personalizada Fig. 10: Superficie tridimensional con personalización avanzada de colores y estilos

Efectos de Iluminación

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LightSource

# Crear datos
x = np.linspace(-5, 5, 50)
y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2)) * np.exp(-(X**2 + Y**2) / 50)

fig = plt.figure(figsize=(16, 12))

# Diferentes configuraciones de iluminación
configs_iluminacion = [
    {'vert_exag': 1, 'azdeg': 315, 'altdeg': 45, 'blend_mode': 'soft'},
    {'vert_exag': 2, 'azdeg': 45, 'altdeg': 60, 'blend_mode': 'hsv'},
    {'vert_exag': 0.5, 'azdeg': 135, 'altdeg': 30, 'blend_mode': 'overlay'},
    {'vert_exag': 1.5, 'azdeg': 225, 'altdeg': 75, 'blend_mode': 'soft'}
]

titulos = ['Iluminación 1', 'Iluminación 2', 'Iluminación 3', 'Iluminación 4']

for i, (config, titulo) in enumerate(zip(configs_iluminacion, titulos)):
    ax = fig.add_subplot(2, 2, i+1, projection='3d')

    # Crear fuente de luz
    ls = LightSource(**config)

    # Calcular colores con iluminación
    rgb = ls.shade(Z, cmap=plt.cm.viridis, vert_exag=config['vert_exag'],
                   blend_mode=config['blend_mode'])

    # Crear superficie con iluminación
    ax.plot_surface(X, Y, Z, facecolors=rgb, linewidth=0, antialiased=True)

    ax.set_title(titulo)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')

plt.tight_layout()
plt.show()

Múltiples Subplots 3D

Aprende a organizar y comparar múltiples gráficos 3D en una sola figura utilizando subplots. Esta sección te enseñará layouts básicos con grids regulares, así como diseños complejos con GridSpec para crear dashboards informativos que permitan análisis comparativos efectivos de diferentes visualizaciones tridimensionales.

Organizar múltiples gráficos 3D en una figura.

Subplots 3D Básicos

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

# Crear datos
x = np.linspace(-3, 3, 30)
y = np.linspace(-3, 3, 30)
X, Y = np.meshgrid(x, y)

fig = plt.figure(figsize=(16, 12))

# Subplot 1: Superficie
ax1 = fig.add_subplot(2, 2, 1, projection='3d')
Z1 = np.sin(np.sqrt(X**2 + Y**2))
surf1 = ax1.plot_surface(X, Y, Z1, cmap='viridis', alpha=0.8)
ax1.set_title('Superficie')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')

# Subplot 2: Wireframe
ax2 = fig.add_subplot(2, 2, 2, projection='3d')
Z2 = X**2 - Y**2
wire2 = ax2.plot_wireframe(X, Y, Z2, color='red', alpha=0.8)
ax2.set_title('Wireframe')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')

# Subplot 3: Scatter 3D
ax3 = fig.add_subplot(2, 2, 3, projection='3d')
np.random.seed(42)
scatter_x = np.random.normal(0, 2, 100)
scatter_y = np.random.normal(0, 2, 100)
scatter_z = np.random.normal(0, 2, 100)
scatter3 = ax3.scatter(scatter_x, scatter_y, scatter_z, c=scatter_z, cmap='plasma')
ax3.set_title('Dispersión 3D')
ax3.set_xlabel('X')
ax3.set_ylabel('Y')
ax3.set_zlabel('Z')

# Subplot 4: Contorno 3D
ax4 = fig.add_subplot(2, 2, 4, projection='3d')
Z4 = np.exp(-(X**2 + Y**2) / 4)
surf4 = ax4.plot_surface(X, Y, Z4, cmap='inferno', alpha=0.6)
cont4 = ax4.contour(X, Y, Z4, levels=8, colors='black', alpha=0.5)
ax4.set_title('Contorno 3D')
ax4.set_xlabel('X')
ax4.set_ylabel('Y')
ax4.set_zlabel('Z')

plt.tight_layout()
plt.show()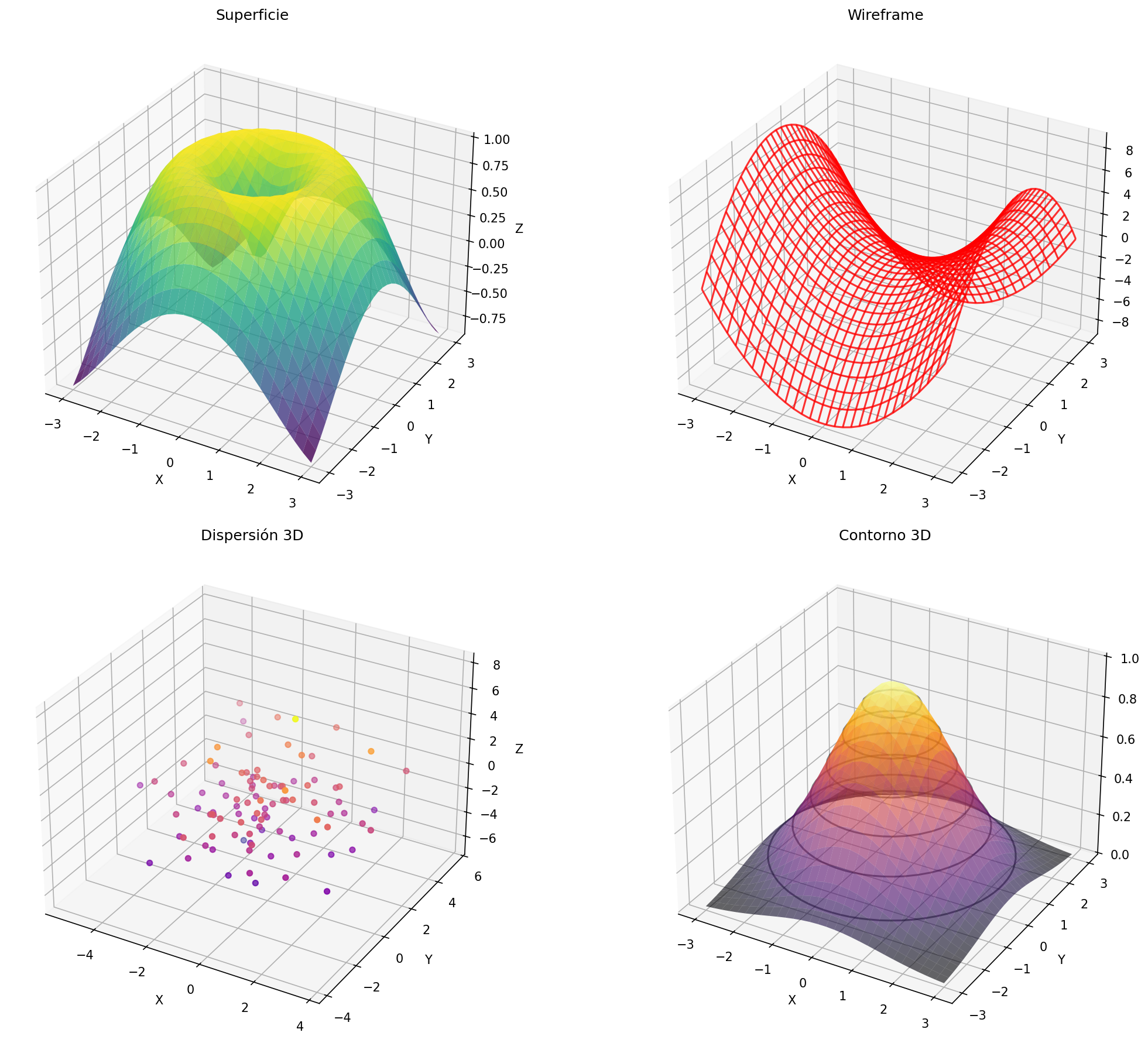

Múltiples Subplots 3D Fig. 11: Múltiples gráficos 3D organizados en subplots

Layouts 3D Complejos

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.gridspec as gridspec

fig = plt.figure(figsize=(18, 12))

# GridSpec para layout complejo
gs = gridspec.GridSpec(3, 4, figure=fig, wspace=0.3, hspace=0.4)

# Gráfico principal (ocupa 2x3)
ax_main = fig.add_subplot(gs[:2, :3], projection='3d')
x = np.linspace(-4, 4, 40)
y = np.linspace(-4, 4, 40)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)
surf_main = ax_main.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax_main.set_title('Gráfico Principal', fontsize=14, fontweight='bold')

# Gráfico derecho superior
ax_top_right = fig.add_subplot(gs[0, 3], projection='3d')
sphere_u = np.linspace(0, 2*np.pi, 20)
sphere_v = np.linspace(0, np.pi, 20)
sphere_x = np.outer(np.cos(sphere_u), np.sin(sphere_v))
sphere_y = np.outer(np.sin(sphere_u), np.sin(sphere_v))
sphere_z = np.outer(np.ones(np.size(sphere_u)), np.cos(sphere_v))
ax_top_right.plot_surface(sphere_x, sphere_y, sphere_z, color='red', alpha=0.6)
ax_top_right.set_title('Esfera')

# Gráfico derecho medio
ax_mid_right = fig.add_subplot(gs[1, 3], projection='3d')
t = np.linspace(0, 4*np.pi, 100)
helix_x = np.sin(t)
helix_y = np.cos(t)
helix_z = t / (2*np.pi)
ax_mid_right.plot(helix_x, helix_y, helix_z, 'b-', linewidth=2)
ax_mid_right.set_title('Hélice')

# Gráficos inferiores (2x4)
ax_bottom_left = fig.add_subplot(gs[2, :2], projection='3d')
np.random.seed(42)
scatter_x = np.random.normal(0, 2, 200)
scatter_y = np.random.normal(0, 2, 200)
scatter_z = np.random.normal(0, 2, 200)
ax_bottom_left.scatter(scatter_x, scatter_y, scatter_z, c=scatter_z, cmap='plasma', alpha=0.6)
ax_bottom_left.set_title('Dispersión 3D')

ax_bottom_right = fig.add_subplot(gs[2, 2:], projection='3d')
bars_x = [1, 2, 3, 4]
bars_y = [1, 1, 1, 1]
bars_z = [0, 0, 0, 0]
bars_dx = [0.8, 0.8, 0.8, 0.8]
bars_dy = [0.8, 0.8, 0.8, 0.8]
bars_dz = [2, 3, 1.5, 4]
ax_bottom_right.bar3d(bars_x, bars_y, bars_z, bars_dx, bars_dy, bars_dz,
                     color='skyblue', alpha=0.8)
ax_bottom_right.set_title('Barras 3D')

plt.show()

Animaciones 3D

Descubre el fascinante mundo de las animaciones tridimensionales para crear visualizaciones dinámicas que evolucionan con el tiempo. Aprenderás a generar animaciones de rotación, ondas propagándose, trayectorias de partículas y otros efectos dinámicos que harán que tus presentaciones cobren vida y permitan una comprensión más profunda de fenómenos temporales.

Crear animaciones interactivas en 3D.

Animación Básica de Rotación

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation

# Crear datos
x = np.linspace(-3, 3, 30)
y = np.linspace(-3, 3, 30)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# Función de inicialización
def init():
    ax.clear()
    surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title('Animación 3D - Rotación')
    return surf,

# Función de animación
def animate(frame):
    ax.clear()
    ax.view_init(elev=20, azim=frame)
    surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title('.1f')
    return surf,

# Crear animación
anim = FuncAnimation(fig, animate, init_func=init, frames=np.arange(0, 360, 2),
                    interval=50, blit=False)

# Para guardar la animación (requiere ffmpeg)
# anim.save('rotacion_3d.gif', writer='pillow', fps=20)

plt.show()

Animación de Onda Propagándose

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation

# Crear datos base
x = np.linspace(-5, 5, 40)
y = np.linspace(-5, 5, 40)
X, Y = np.meshgrid(x, y)

fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# Función de inicialización
def init():
    ax.clear()
    Z = np.sin(np.sqrt(X**2 + Y**2))
    surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title('Onda Propagándose')
    ax.set_zlim(-2, 2)
    return surf,

# Función de animación
def animate(frame):
    ax.clear()
    # Onda que se propaga desde el centro
    r = np.sqrt(X**2 + Y**2)
    Z = np.sin(r - frame * 0.1) / (r + 1)  # Amortiguada
    surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title('.1f')
    ax.set_zlim(-2, 2)
    return surf,

# Crear animación
anim = FuncAnimation(fig, animate, init_func=init, frames=100,
                    interval=50, blit=False)

plt.show()

¡Has completado el tutorial completo de gráficos 3D con Matplotlib! Ahora puedes crear visualizaciones tridimensionales impresionantes que revelan patrones complejos en tus datos.

Experimenta con diferentes tipos de gráficos 3D y anima tus visualizaciones para presentaciones impactantes. La visualización 3D es una herramienta poderosa para el análisis de datos científicos y técnicos.