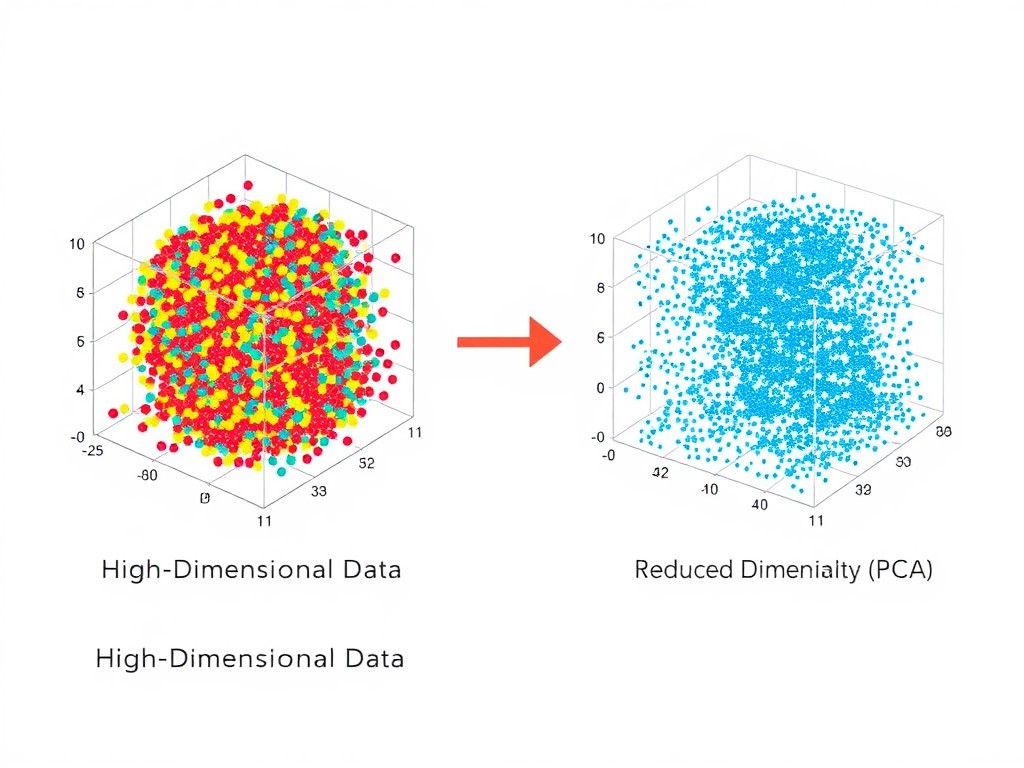
El Análisis de Componentes Principales (PCA, por sus siglas en inglés) es una técnica estadística utilizada para reducir la dimensionalidad de un conjunto de datos, preservando la mayor cantidad posible de la varianza original. Es especialmente útil en el análisis exploratorio de datos, la compresión de datos y la visualización, así como en la mejora del rendimiento de algoritmos de aprendizaje automático.

¿Qué es PCA?

El PCA transforma un conjunto de variables correlacionadas en un conjunto de variables no correlacionadas, denominadas componentes principales. Estas componentes son ortogonales entre sí y están ordenadas de tal manera que la primera componente principal captura la mayor parte de la variabilidad de los datos, la segunda componente captura la segunda mayor parte de la variabilidad, y así sucesivamente.

Propósito del PCA

1. Reducción de Dimensionalidad
2. Eliminación de Ruido
3. Visualización: Permite visualizar datos en 2D o 3D, facilitando la identificación de patrones y relaciones.

Proceso de PCA

1. Estandarización de los Datos: Los datos deben ser estandarizados (normalizados) para que cada variable tenga una media de 0 y una desviación estándar de 1. Esto es crucial, especialmente si las variables están en diferentes escalas.
2. Cálculo de la Matriz de Covarianza: Se calcula la matriz de covarianza para entender cómo varían las variables en relación entre sí.
3. Cálculo de los Valores y Vectores Propios: Se determinan los valores propios y los vectores propios de la matriz de covarianza. Los valores propios indican la cantidad de varianza que captura cada componente, y los vectores propios indican la dirección de esos componentes.
4. Selección de Componentes Principales: Se seleccionan los componentes principales en función de sus valores propios, eligiendo aquellos que capturan la mayor parte de la varianza.
5. Transformación de los Datos: Los datos originales se proyectan en el nuevo espacio definido por los componentes principales seleccionados.

En python mediante la libreria scikit-learn, se puede obtener los últimos pasos con PCA. A continuación un código de ejemplo.

# importamos las librerias necesarias
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# Cargar el conjunto de datos Iris
# Este conjunto de datos es ideal para funciones de clasificación y agrupamiento
iris = load_iris()
X = iris.data  # Características
y = iris.target  # Etiquetas de clase


# Proceso 1. Estandarizar los datos
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Proceso 2,3,4,5. Aplicar PCA y transformar los datos
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# Proceso 5. Crear un DataFrame para los datos transformados
df = pd.DataFrame(data=X_pca, columns=['Componente 1', 'Componente 2'])
df['Clase'] = iris.target

# Graficar
plt.figure(figsize=(8, 6))
scatter = plt.scatter(df['Componente 1'], df['Componente 2'], c=df['Clase'], cmap='viridis')
plt.title('PCA de Iris Dataset')
plt.xlabel('Componente 1')
plt.ylabel('Componente 2')
plt.colorbar(scatter, label='Clase')
plt.grid()
plt.show()

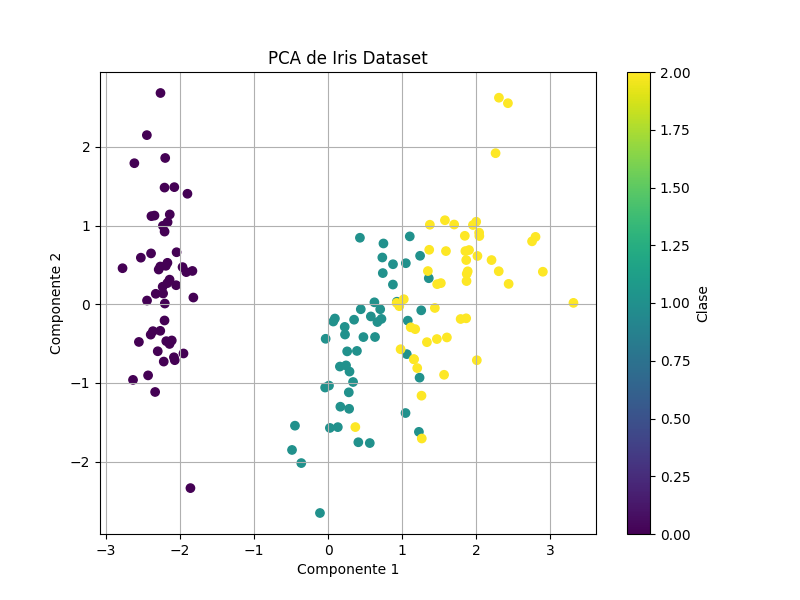
El Análisis de Componentes Principales es una herramienta poderosa en el análisis de datos. Su capacidad para reducir la dimensionalidad y facilitar la visualización lo convierte en una técnica esencial en la ciencia de datos y el aprendizaje automático. Sin embargo, es importante ser consciente de sus limitaciones y de la posible pérdida de información al aplicar esta técnica. Con un uso adecuado, PCA puede proporcionar valiosos insights y mejorar el rendimiento en diversas aplicaciones.